Đáp án A.
Cách giải:
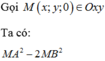
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.
Đáp án A.
Cách giải:
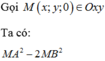
![]()
Thử lần lượt 4 đáp án thì ta thấy với M(3;-4;0)
thì M A 2 - 2 M B 2 = 3 là lớn nhất.
Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; 1; -3). Tìm điểm M trên mặt phẳng (Oxy) sao cho M A 2 - 2 M B 2 lớn nhất.
A . M 3 2 ; 1 2 ; 0
B . M 1 2 ; - 3 2 ; 0
C. M (0; 0; 5)
D. M (3; -4; 0)
Trong không gian Oxyz, cho hai điểm A(1;2;1), B(2;-1;3) và điểm M(a;b;0) sao cho M A 2 + M B 2 nhỏ nhất. Giá trị của a+b bằng
A. 3
B. 2
C. 1
D. -2
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;0;1), B(1;2;1), C(4;1;-2) và mặt phẳng P : x + y + z = 0 . Tìm trên (P) điểm M sao cho M A 2 + M B 2 + M C 2 đạt giá trị nhỏ nhất. Khi đó M có tọa độ:
A. M(1;1;-1)
B. M(1;1;1)
C. M(1;2;-1)
D. M(1;0;-1)
Trong không gian Oxyz, cho hai điểm A(5;7;6) và B(2;4;3). Trên mặt phẳng (Oxy), lấy điểm M(a;b;c) sao cho MA + MB bé nhất. Tính P = a 2 + b 3 + c 4
A. P = 134
B. P = -122
C. P = -204
D. P = 52
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;2;-1),B(-2:-4;3),C(1;3;-1). Tìm điểm M ∈ O x y sao cho M A → + M B → + 3 M C → đạt giá trị nhỏ nhất.
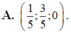
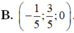
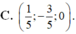
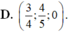
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; -2; -1), B (-2,-4,3), C (1;3;-1) và mặt phẳng (P): x + y -2z – 3 = 0. Tìm điểm M ∈ (P) sao cho M A → + M B → + 2 M C → đạt giá trị nhỏ nhất.
A . M 1 2 ; 1 2 ; - 1
B . M - 1 2 ; - 1 2 ; 1
C . M 2 ; 2 ; - 4
D . M - 2 ; - 2 ; 4
Trong không gian Oxyz, cho hai điểm A(-1;3;-2), B(-3;7;-18) và mặt phẳng (P): 2x-y+z+1=0. Điểm M(a;b;c) thuộc (P) sao cho mặt phẳng (ABM) vuông góc với (P) và M A 2 + M B 2 = 246 . Tính S = a+b+c
A. 0
B. -1
C. 10
D. 13
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2
Trong không gian Oxyz, cho hai điểm A ( 1 ; 2 ; 1 ) , B ( 2 ; - 1 ; 2 ) . Điểm M trên trục Ox và cách đều hai điểm A, B có tọa độ là
A. M 1 2 ; 0 ; 0
B. M - 1 2 ; 0 ; 0
C. M 3 2 ; 0 ; 0
D. M 0 ; 1 2 ; 3 2