Cho tam giác MNP vuông tại N. Trên tia đối của tia PN lấy điểm Q. So sánh độ dài MP và MQ.

Những câu hỏi liên quan
1)So sánh các cạnh của Tam giác ABC biết A 80° B40°2)Sosánh các cạnh của Tam giác PQR biết P 70° R 50°3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC 4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ5) Cho tam giác ABC có ba góc nhọn AB AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của BC và CE . So sánh độ dài của HB và HC
Đọc tiếp
1)So sánh các cạnh của Tam giác ABC biết A= 80° B=40°
2)Sosánh các cạnh của Tam giác PQR biết P = 70° R= 50°
3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC
4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ
5) Cho tam giác ABC có ba góc nhọn AB < AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của BC và CE . So sánh độ dài của HB và HC
Cho tam giác MNP có góc M>90 độ. Trên tia đối của tia PN lấy điểm Q.
a)so sánh MN và MP.
b)Chứng minh tam giác MNQ là tam giác tù.
c)Chứng minh MN<MP<MQ
cho tam giác MNP có M=80, N=40 a, so sánh các cạnh của tam giác MNP b, trên tia đối của tia MN lấy điểm D sao cho MD=MP , trên tia đối của tia NM lấy điểm E sao cho NE=NP. so sánh đoạn thẳng PD PN PE
cho tam giác mnp vuông tại m đường trung tuyến pq a cho bt np=10cm mp=6cm.
a)tính độ dài đoạn thẳng mn,nq
b) trên tia đối của tia qp lấy điểm d sao cho qd =qp
cm tam giác qmp= tam giác qnd và mp=nd
c) cmr mp+np > 2qp
d) gọi k là điểm trên đoạn thẳng mq sao cho mk=2/3mq
gọi h là giao điểm của pk và md
y là giao điểm của nh và pd
cmr pd=3yd
a: \(MN=\sqrt{NP^2-MP^2}=8\left(cm\right)\)
nên NQ=4(cm)
b: Xét ΔQMP và ΔQND có
QM=QN
\(\widehat{MQP}=\widehat{NQD}\)
QP=QD
Do đó; ΔQMP=ΔQND
Suy ra: MP=ND
Đúng 0
Bình luận (0)
cho tam giác mnp vuông tại m (mp<mn) trên cạnh mn lấy điểm q sao cho mq=mp trên tia đối của tia mp lấy điểm r sao cho mr=mn chứng minh :
a) pq vuông góc nr b) rq vuông góc np
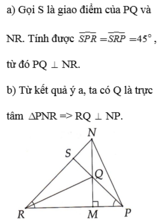
Cho tam giác MNP vuông tại M (MP < MN). Trên cạnh MN lấy điểm Q sao cho MQ = MP, trên tia đối của tia MP lấy điểm R sao cho MR = MN. Chứng minh:
a) P Q ⊥ N R .
b) R Q ⊥ N P .
Cho tam giác MNP cân tại M, trên tia đối của tia MP lấy điếm K, trên tia đối của tia MN lấy điểm H sao cho MK=MH
a.Cm: tam giác MKH cân
b.CM: tam giác KMN= tam giác HMP
c. gọi Q là trung điểm của HK. CM: MQ vuông góc với HK
d. CM: HK song song với NP
a: Xét ΔMKH có MK=MH
nên ΔMKH cân tại M
b: Xét ΔKMN và ΔHMP có
MK=MH
\(\widehat{KMN}=\widehat{HMP}\)
MN=MP
Do đó: ΔKMN=ΔHMP
c: Ta có: ΔMKH cân tại M
mà MQ là đường trung tuyến
nên MQ là đường cao
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M, MH vuông góc NP tại H, trên NP lấy Q sao cho NQ=MN. Đường vuông góc với NP tại Q cắt MP tại R. CM:
a)MR=RQ
b)MQ là tia phân giác của góc HMP
c)Gọi Px là tia đối của tia PN, đường phân giác của góc MPx cắt NR tại K. Tính góc NMK
d)MN+MP<NP+MH
giúp em đi ạ
Cho tam giác MNP cân tại M, trên tia đối của tia MP lấy điếm K, trên tia đối của tia MN lấy điểm H sao cho MK=MH
a.Cm: tam giác MKH cân
b.CM: tam giác KMN= tam giác HMP
c. gọi Q là trung điểm của HK. CM: MQ vuông góc với HK
d. CM: HK song song với NP
a: Xét ΔMKH có MK=MH
nên ΔMKH cân tại M
b: Xét ΔKMN và ΔHMP có
MK=MH
\(\widehat{KMN}=\widehat{HMP}\)
MN=MP
Do đó: ΔKMN=ΔHMP
c: Ta có: ΔMKH cân tại M
mà MQ là đường trung tuyến
nên MQ là đường cao
Đúng 0
Bình luận (0)