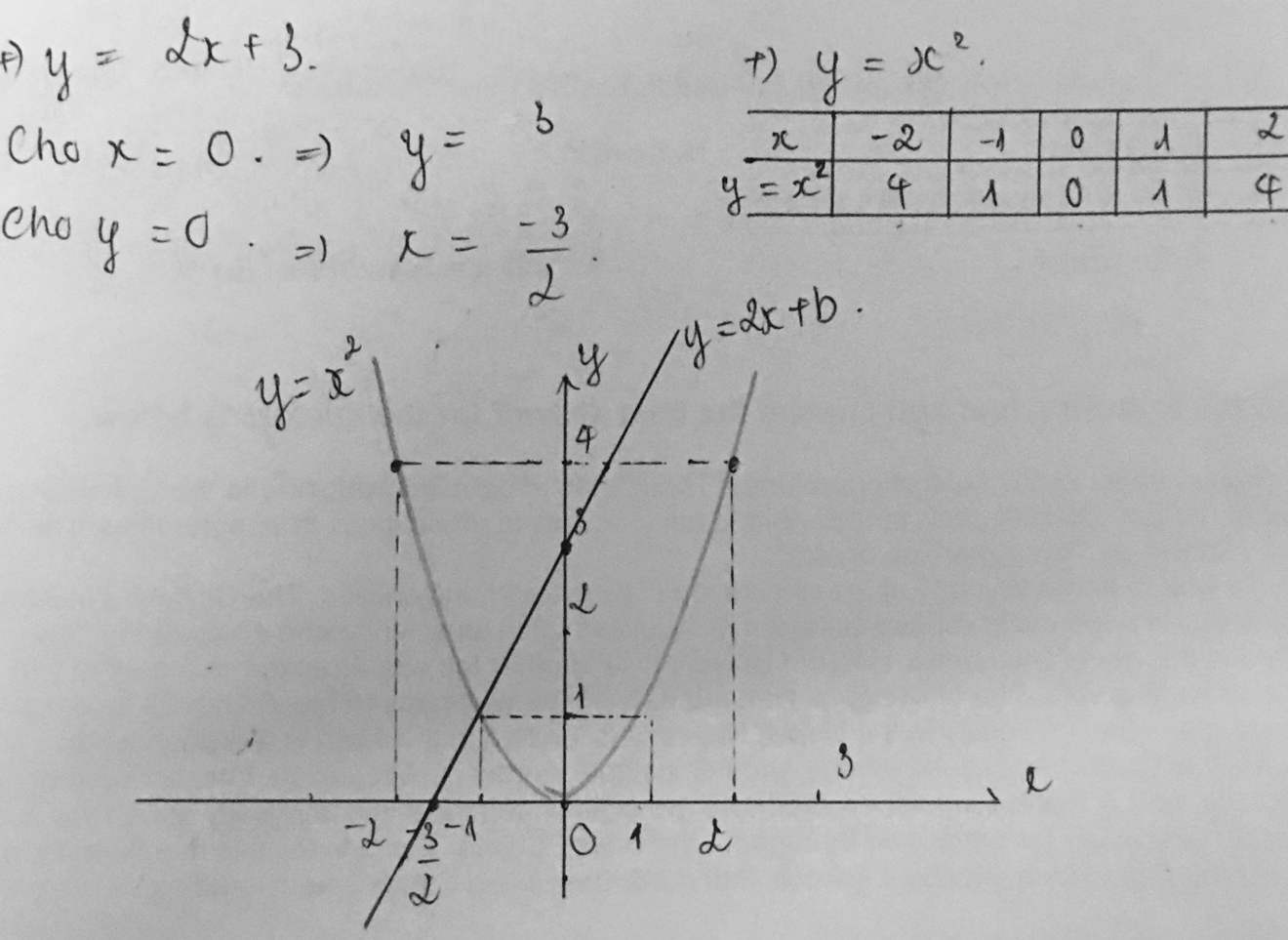Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).

Những câu hỏi liên quan
a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y=-2x 5(d1);y=x+2(d2)
b) Tìm tọa độ giao điểm M của hai đường thẳng (d1) và (d2)
\(b,\) PT hoành độ giao điểm: \(-2x+5=x+2\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow M\left(1;3\right)\)
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, vẽ đồ thị của hàm số y = x.
b) Trên mặt phẳng tọa độ Oxy, vẽ đồ thị của hàm số y = 2x.
giúp mình với ạ:'D
a, Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau : yx+2 và y-2x + 5b, Gọi giao điểm của các đường thẳng y x+2 và y -2x+5 với trục hoành theo thứ tự là A và B , gọi giao điểm của 2 đường thẳng trên là C.Tìm tọa độ của điểm C.Tính Chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là cm và làm tròn đến chữ số thập phân thứ 2 ) Các bác jup e vs
Đọc tiếp
a, Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau : y=x+2 và y=-2x + 5
b, Gọi giao điểm của các đường thẳng y = x+2 và y = -2x+5 với trục hoành theo thứ tự là A và B , gọi giao điểm của 2 đường thẳng trên là C.Tìm tọa độ của điểm C.Tính Chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là cm và làm tròn đến chữ số thập phân thứ 2 )
Các bác jup e vs
b) Vì C(xC,yC) là giao điểm của hai đường thẳng y=x+2 và y=-2x+5 nên hoành độ của C là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của y=x+2 và y=-2x+5
hay x+2=-2x+5
\(\Leftrightarrow x+2+2x-5=0\)
\(\Leftrightarrow3x-3=0\)
\(\Leftrightarrow3x=3\)
hay x=1
Thay x=1 vào hàm số y=x+2, ta được:
y=1+2=3
Vậy: C(1;3)
Vì A(xA;yA) là giao điểm của đường thẳng y=x+2 với trục hoành nên yA=0
Thay y=0 vào hàm số y=x+2, ta được:
x+2=0
hay x=-2
Vậy: A(-2:0)
Vì B(xB,yB) là giao điểm của đường thẳng y=-2x+5 với trục hoành Ox nên yB=0
Thay y=0 vào hàm số y=-2x+5, ta được:
-2x+5=0
\(\Leftrightarrow-2x=-5\)
hay \(x=\dfrac{5}{2}\)
Vậy: \(B\left(\dfrac{5}{2};0\right)\)
Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(xA-xB\right)^2+\left(yA-yB\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(-2-\dfrac{5}{2}\right)^2+\left(0-0\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(-\dfrac{9}{2}\right)^2}=\dfrac{9}{2}=4,5\left(cm\right)\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(xA-xC\right)^2+\left(yA-yC\right)^2}\)
\(\Leftrightarrow AC=\sqrt{\left(-2-1\right)^2+\left(0-3\right)^2}\)
\(\Leftrightarrow AC=\sqrt{18}=3\sqrt{2}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(xB-xC\right)^2+\left(yB-yC\right)^2}\)
\(\Leftrightarrow BC=\sqrt{\left(\dfrac{5}{2}-1\right)^2+\left(0-3\right)^2}\)
\(\Leftrightarrow BC=\sqrt{\dfrac{45}{4}}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(\Leftrightarrow C_{ABC}=4.5+3\sqrt{2}+\dfrac{3\sqrt{5}}{2}\simeq12.10cm\)
Nửa chu vi của tam giác ABC là:
\(P_{ABC}=\dfrac{C_{ABC}}{2}\simeq\dfrac{12.10}{2}=6.05cm\)
Diện tích của tam giác ABC là:
\(S_{ABC}=\sqrt{P\cdot\left(P-AB\right)\cdot\left(P-BC\right)\cdot\left(P-AC\right)}\)
\(=\sqrt{6.05\cdot\left(6.05-4.5\right)\cdot\left(6.05-3\sqrt{2}\right)\cdot\left(6.05-\dfrac{3\sqrt{5}}{2}\right)}\)
\(\simeq6.76cm^2\)
Đúng 1
Bình luận (1)
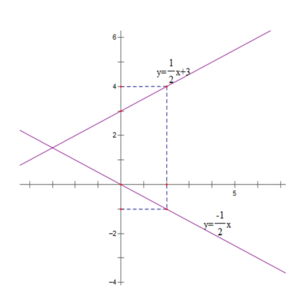
a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:
y = - 1 2 x d 1 v à y = 1 2 x + 3 d 2
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 2 |
| y = -1/2 x | 0 | - 1 |
| y = 1/2 x + 3 | 3 | 4 |
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ
Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
b
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ
Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
b
Đúng 0
Bình luận (0)
Cho hàm số y=\(x^2\) và y=2x+3
vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ.
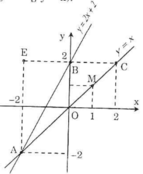
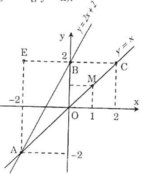
Câu 14(1,5 điểm): a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = - 2x + 5 ; y = x + 2 b) Tìm tọa độ giao điểm A của đường thẳng y = - 2x + 5 và y=x+2. c) Tính góc tạo bởi đường thẳng y = x + 2y với trục Ox. d) Xác định đường thẳng y = ax + b đi qua điểm A và song song với đường thẳng y = - 3x - 1
a:
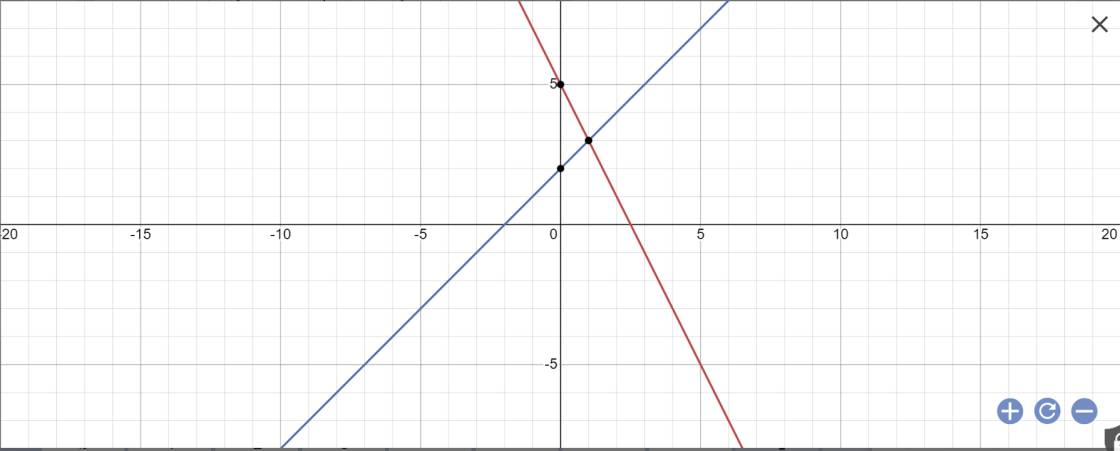
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6
Đúng 0
Bình luận (0)
cho hàm số : y=x\(^2\)và y=-2x+3
a) vẽ đồ thị của hàm số trên cùng mặt phẳng tọa độ Oxy.
b) tìm tọa độ các giao điểm của hai đồ thị trên
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=-2x+3\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+2x-3=0\\y=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-3;9\right);\left(1;1\right)\right\}\)
Đúng 1
Bình luận (1)