Cho tam giác ABC . Gọi D là điểm sao cho B D → = 2 3 B C → và I là trung điểm của cạnh AD , M là điểm thỏa mãn A M → = 2 5 A C → Vectơ B I → được phân tích theo hai vectơ B A → v à B C → .Hãy chọn khẳng định đúng trong các khẳng định sau?
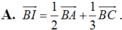
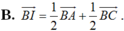
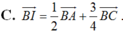
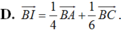
Câu 11. Cho tam giác ABC, lấy điểm D sao cho B là trung điểm của đoạn thẳng AD. Kẻ
đường thẳng d đi qua D và song song với AC, d cắt BC tại E.
1. Chứng minh: tam giác ABC=tam giác DBE
2. Chứng minh: BC = BE, AE // CD
3. Gọi M là trung điểm của đoạn thẳng AC, N là trung điểm của đoạn thẳng DE. Chứng
minh 3 điểm M, B, N thẳng hàng
(Lưu ý vẽ hình)
1/ Xét tg ABC và tg DBE có
BA=BD (gt)
DE//AC (gt) \(\Rightarrow\widehat{BAC}=\widehat{BDE}\) (góc so le trong)
\(\widehat{ABC}=\widehat{DBE}\) (góc đối đỉnh)
=> tg ABC = tg DBE (g.c.g)
2/
Ta có tg ABC = tg DBE (cmt) => BC=BE
Xét tư giác ACDE có
BA=BD (gt); BC=BE (cmt) => ACDE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AE//CD (cạnh đối hbh)
3/
Xét tg ADC có
MA=MC (gt); BA=BD (gt) => BM là đường trung bình của tg ADC
=> BM//CD
Xét tg ADE có
BA=BD (gt); NE=ND (gt) => BN là đường trung bình của tg ADE
=> BN//AE
Mà CD//AE (cạnh đối hbh)
=> BM//AE (cùng //CD)
\(\Rightarrow BN\equiv BM\) (từ 1 điểm ngoài đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
=> M, B, N thẳng hàng
cho tam giác ABC. Gọi D là trung điểm AC. Gọi E là trung điểm BD. Lấy điểm F sao cho D là trung điểm EF. Gọi G là trung điểm BC. Lấy điểm M sao cho G là trung điểm EM. Chứng minh rằng:
a)DF = CM
b) AF = BM
c) tam giác MEC = tam giác DAF
d) GE song song BM và GE = 1/2 DC
a: Xét ΔGEB và ΔGMC có
GE=GM
\(\widehat{EGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGEB=ΔGMC
=>CM=BE
mà BE=ED=DF
nên DF=CM
b: Xét ΔDAF và ΔDCE có
DA=DC
\(\widehat{ADF}=\widehat{CDE}\)
DF=DE
Do đó: ΔDAF=ΔDCE
=>AF=CE(1)
Xét ΔGEC và ΔGMB có
GE=GM
\(\widehat{EGC}=\widehat{MGB}\)(hai góc đối đỉnh)
GC=GB
Do đó: ΔGEC=ΔGMB
=>EC=MB(2)
Từ (1) và (2) suy ra AF=BM
c: Xét ΔGEB và ΔGMC có
GE=GM
\(\widehat{EGB}=\widehat{MGC}\)(hai góc đối đỉnh)
GB=GC
Do đó: ΔGEB=ΔGMC
=>EB=MC
Xét ΔEBM và ΔMCE có
EB=MC
EM chung
BM=CE
Do đó: ΔEBM=ΔMCE
=>\(\widehat{EBM}=\widehat{MCE}\)(3)
Ta có: ΔGEC=ΔGMB
=>\(\widehat{GEC}=\widehat{GMB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EC//BM
=>\(\widehat{DEC}=\widehat{EBM}\)(hai góc đồng vị)(4)
Ta có: ΔDEC=ΔDFA
=>\(\widehat{DEC}=\widehat{DFA}\)(5)
Từ (3),(4),(5) suy ra \(\widehat{ECM}=\widehat{AFD}\)
Xét ΔMEC và ΔDAF có
CE=FA
\(\widehat{ECM}=\widehat{AFD}\)
CM=FD
Do đó: ΔMEC=ΔDAF
d: Xét ΔBDC có
G,E lần lượt là trung điểm của BC,BD
=>GE là đường trung bình của ΔBDC
=>GE//DC và \(GE=\dfrac{DC}{2}\)
Cho ABC có B B = 60 , A = 2 cm,BC = 5 cm. Trên cạnh BC lấy điểm D sao cho
BA BD = .
a) Chứng minh tam giác ABD đều;
b) Gọi H là trung điểm của BD. Chứng minh AH BD ⊥ ;
c) Tính độ dài cạnh AC;
d) Tam giác ABC có là tam giác vuông không? Tại sao?
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE=1/3 BE
a) so sánh diện tích tam giác abe với diện tích tam giác abc
b) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2
c) tính diện tích tứ giác abced
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE=1/3 BE
a) so sánh diện tích tam giác abe với diện tích tam giác abc
b) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2
c) tính diện tích tứ giác abced
Cho tam giác abc . gọi D là trung điểm của ab .trên cạnh bc lấy điểm E sao cho CE=1/3 BE
a) so sánh diện tích tam giác abe với diện tích tam giác abc
b) tính diện tích tam giác abc biết diện tích tam giác bde là 12 cm2
c) tính diện tích tứ giác abced
xin lỗi mọi người là tính tứ giác aced chứ ko phải acbed
Giải:
a) Diện tích tam giác ABC = 1/2 x AH x BC
Diện tích tam giác ABE = 1/2 x AH x BE
= 1/2 x AH x 2/3 BC
= 1/2 x AH x BC x 2/3
= Diện tích tam giác ABC x 2/3
Vậy: Diện tích tam giác ABE = 2/3 diện tích tam giác ABC.
b) Vì chiều cao DE có D là trung điểm nên Diện tích tam giác ABE = 2 lần diện tích tam giác BDE
= 12 x 2
= 24
Diện tích tam giác ABC = 24 : 2/3
= 36
c) Diện tích hình tứ giác ADEC là: 36 - 24 = 12 ( cm vuông)
Đáp số: ...........................
Giải
Chiều cao là:
15 x 2/6=6 (cm)
Diện tích tam giác ABC là:
7 x 6/2 =21 (cm2
)
Đáp số
Cho tam giác ABC có A=90 độ . Trên tia đối tia AB lấy D sao cho AB=AD . Trên tia đối tia AC lấy E sao cho AC=AE .
a) Chứng minh tam giác ABC=tam giác ADE .
b) Chứng minhED=BC .
c) Gọi I là trung điểm DC . Chứng minh DI=1/2 BC .
d) Gọi N là giao điểm CA vad BI . Mlaf trung điểm BC . Chứng minh D,N,M thảng hàng .
mọi người giúp mình với . Cảm ơn nhiều
b: Xét tứ giác DECB có
A là trung điểm của CD
A là trung điểm của EB
Do đó: DECB là hình bình hành
Suy ra: ED=BC
Trong mpOxy, cho tam giác ABC có A(1; 1), B(3; 3), C(0;-6).
1,Tính cos A.
2,Tìm tọa độ điểm D sao cho tam giác ABD vuông cân tại D.
3,Gọi E là chân đường phân giác trong của góc A.Tìm tọa độ điểm E.
Cho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm D, E sao cho AD = DE = EM. Gọi O là trung điểm của đoạn thẳng DE. Khi đó trọng tâm của tam giác ABC là:
(A) Điểm D
(B) Điểm E
(C) Điểm O
(D) Cả (A), (B), (C) đều sai
Trên đường trung tuyến AM có AD = DE = EM nên AE = 2/3 AM.
Do khoảng cách từ trọng tâm tới một đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó nên E là trọng tâm của tam giác ABC. Chọn (B) Điểm E.
Cho Tam giác ABC có góc B=60 .Trên Cạnh AC Lấy D sao cho góc ABD=1/3 góc ABC trên cạnh AB lấy E sao cho góc ACE =1/3 ACB .Gọi F là giao điểm của BD và CE .a)tính góc ACE.
b) gọi I và k theo thứ tự là chân đg vuông góc kẻ từ F xuống BC Tại AC , G và H là 2 điểm lần lượt trên tia đối FI và FK .Sao cho I là trung điểm .K là trung điểm của FH.C.m tam giác CGH là tam giác đều.
c)c/m 3 điểm H,D,G thẳng hàng
Bài 2. Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho AD = AE. a) Chứng minh rằng: BE = CD b) Chứng minh rằng: góc ABE bằng góc ACD c) Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao? d) Gọi I là trung điểm BC. Chứng minh A, K, I thẳng hàng
a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng