Cho tam giác ABC, điểm I thoả mãn 5 M A → = 2 M B → Nếu I A → = m I M → + n I B → thì cặp số (m; n) bằng:
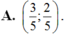
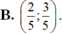
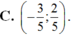
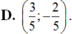
Cho tam giác ABC, điểm I thoả mãn: 5 M A → = 2 M B → . Nếu I A → = m I M → + n I B → thì cặp số (m; n) bằng:
A. 
B. 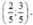
C. 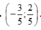
D. 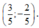
cho tam giác abc m là trung điểm của bc, I trung điểm Am.Tìm hai số thực m,n thoả mãn AI=mCA+nCB
vecto AI=1/2*vecto AM
=1/4(vecto AB+vecto AC)
=1/4(vecto AC+vecto CB+vecto AC)
=1/4(-2vecto CA+vecto CB)
=-1/2*vecto CA+1/4*vecto CB
=>m=-1/2; n=1/4
Cho tam giác ABC, trên cạnh BC lấy điểm D sao cho BD= 2/3 BC, M là trung điểm của đoạn thẳng AD, điểm N thoả mãn điều kiện vectơ AN = 2/5 vectơ AC. Chứng minh 3 điểm B , M ,N thẳng hàng.
Xét ΔBAD có BM là đường trung tuyến
nên \(\overrightarrow{BM}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{5}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{6}\left(5\overrightarrow{BA}+2\overrightarrow{AC}\right)\)
\(=\dfrac{5}{6}\left(\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}\right)\)
\(\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{AN}\)
\(=\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\)
=>\(\overrightarrow{BM}=\dfrac{5}{6}\cdot\overrightarrow{BN}\)
=>B,M,N thẳng hàng
Cho tam giác ABC có M, N di chuyển trên AB, AC( M,N khác A,B,C). của tam giác thoả mãn điều kiện AM.AN=BM.CN. Tìm tập hợp trung điểm K của MN
Cho tam giác ABC có điểm M thoả mãn |MA-MB-2MC|=|MA-MB|. Khẳng định nào sau đây là đúng?
A.tam giác ABC đều B,tam giác ABC cân tại C
C.tam giác ABC vuông tại C D.tam giác ABC cân tại B
Bài 1: Cho tam giác ABC đều. Trên tia đối tia BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BD=CE=BC
a) C/m: tam giác ACE cân
b) Tính góc DAE
Bài 2: Cho tam giác ABC cân tại A. Trên tia đối tia AC lấy điểm D sao cho AD = AC. C/m tam giác BCD vuông
Bài 3: Cho tam giác ABC cân tại A có góc A= 40 độ. Lấy điểm D khác phía B so với AC thoả mãn góc CAD=60 độ, góc ACD=80 độ. C/m BD vuông góc AC
Cho tam giác ABC vuông tại A. Điểm D trên AC sao cho CD=2AD. Lấy E trên đoạn thẳng BD thoả mãn góc CED=góc ABC. Gọi F là điểm đối xứng của C qua A, K là điểm đối xứng của B qua A . Giao điểm của BD và CK là M. Chứng minh
a. Tứ giác AMCB là hình thang
b. Tam giác AMB đồng dạng với tam giác EBC
c. EF.MC=BC.BE
d. Góc DEF=2 góc ABC