Các câu hỏi tương tự
Cho hình lăng trụ tam giác ABC A'B'C'. Gọi K M N E lần lượt là trung điểm của các cạnh CC' AB AA' và BB' . G là trọng tâm tam giác ABC, I là điểm thuộc đoạn BC sao cho BI = 1/3 BC. CMR
a/ (MNC) // (A'BK)
b/ (MNK) // (A'BC')
c/ ( GKN) // (A'IC')
Giúp mình câu c với ạ
Cho dãy số ( u n ) thoả mãn u n > M với mọi n. Chứng minh rằng nếu l i m u n = a thì a ≤ M
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến M thành B, N thành C. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến B thành M, C thành N. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Số phát biểuđúng là:a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nób) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiếnc) Phép tịnh tiến biến tứ giác thành tứ giác bằng nód) Phép tịnh tiến biến đường tròn thành chính nóe) Phép đồng nhất biến mọi hình thành chính nóf) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kìg) Phép chiếu lên đường thẳng không là phép dời hìnhh) Với bất kì 2 điểm A, B...
Đọc tiếp
Số phát biểuđúng là:
a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó
b) Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó là phép tịnh tiến
c) Phép tịnh tiến biến tứ giác thành tứ giác bằng nó
d) Phép tịnh tiến biến đường tròn thành chính nó
e) Phép đồng nhất biến mọi hình thành chính nó
f) Phép dời hình là 1 phép biến hình không làm thay đồi khoảng cách giữa hai điểm bất kì
g) Phép chiếu lên đường thẳng không là phép dời hình
h) Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có A’B = AB’.
i) Nếu phép dời hình F biến tam giác ABC thành tam giác A’B’C’ thì trọng tâm tam giác ABC biến thành trọng tâm tam giác A’B’C’.
k) Phép tịnh tiến theo vectơ là phép đồng nhất.
l) Nếu phép dời hình biến điểm A thành điểm B ( B ≠ A ) thì nó cũng biến điểm B thành A
m) Nếu phép dời hình biến điểm A thành điểm B và biến điểm B thành điểm C thì AB = BC
A.5
B.6
C.7
D.8
Cho mặt cầu (S) có tâm I, bán kính R5. Một đường thẳng d cắt (S) tại hai điểm M, N phân biệt nhưng không đi qua I. Đặt MN2m Với giá trị nào của m thì diện tích tam giác IMN lớn nhất?
Đọc tiếp
Cho mặt cầu (S) có tâm I, bán kính R=5. Một đường thẳng d cắt (S) tại hai điểm M, N phân biệt nhưng không đi qua I. Đặt MN=2m Với giá trị nào của m thì diện tích tam giác IMN lớn nhất?
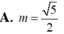
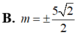
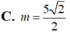
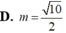
Cho tam giác ABC . Về phía ngoài của tam giác ABC dựng các tam giác đều ABD , ACE , BCF .
a/ C/m BE =CD= AF
b/ I J, lần lượt là trung điểm của các đoạn thẳng BE , CD . Chứng minh tam giác AIJ đều
Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây: A. (ACD) B. (CMN) C. (BCD) D. (ABD)
Đọc tiếp
Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây:
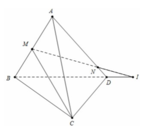
A. (ACD)
B. (CMN)
C. (BCD)
D. (ABD)
cho m>0 và a,b,c là 3 số thực thoả mãn a/m+2 +b/m+1 +c/m=0 Chứng minh rằng phương trình ax^2+bx+c =0 luôn có nghiệm