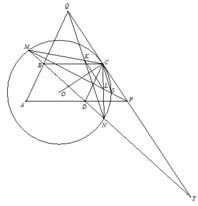
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C.BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
2) CM cắt QN tại K, CN cắt PM tại L. Chứng minh rằng K L ⊥ O C .