Cho hàm số y = ax2 + bx + c có đồ thị (P). Tọa độ đỉnh của (P) là:
A. 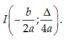
B. 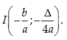
C. 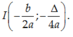
D. 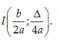
Gọi (P) là đồ thị hàm số y = a x 2 + c . Để đỉnh của (P) có tọa độ (0; -3) và một trong hai giao điểm của (P) với trục hoành là điểm có hoành độ bằng -5 thì:
A. a = 3 25 , c = 3
B. a = - 3 25 , c = - 3
C. a = - 3 25 , c = 3
D. a = 3 25 , c = - 3
cho đồ thị hàm số y=ax2+bx+4 có đỉnh là điểm I(1,-2). Tính a+3b
A.20
B.-18
C.-3-
D.25
Lời giải:
Đỉnh của đths là $(\frac{-b}{2a}, 4-\frac{b^2}{4a})=(1,-2)$
$\Rightarrow \frac{-b}{2a}=1; 4-\frac{b^2}{4a}=-2$
$\Rightarrow -b=2a; b^2=24a$
$\Rightarrow a=0$ hoặc $a=6$
Nếu $a=0$ thì $b=-2a=0$. Khi đó đths $y=4$ là đường thẳng song song với trục hoành, không có đỉnh I(1,-2)$
Nếu $a=6$ thì $b=-2a=-12$. Khi đó: $a+3b=6+3(-12)=-30$
Dùng công thức c - ax² = y cho toạ độ đỉnh ta có :
4 - a.1² = -2
=> a = 6
Thế vào b = -2a ,Ta có :
b = -12
=> a + 3b = 6 - 3.(-12) = -30
Cho hàm số y = x 3 + a x 2 + b x + c b < 0 . Biết rằng đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt đối xứng qua gốc tọa độ. Giá trị của T=2(ab-c)+3 là:
A. T=3
B. T=1
C. T=2
D. T=5
Cho hàm số y = x 3 + ax 2 + bx + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. a = 0
C. a = 3 b
D. ab = 9
Cho hàm số y = x 3 + a x 2 + b x + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. a = 0
C. a = 3b
D. ab = 9
Đáp án D
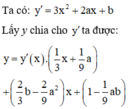
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
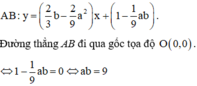
Cho hàm số y = x 3 + a x 2 + b x + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. a = 0
C. a = 3b
D. ab = 9
Đáp án D
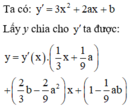
Do đó phương trình đường thẳng đi qua hai điểm cực trị là
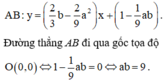
Cho hàm số y = x 3 + ax 2 + bx + 1 và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ O 0 ; 0 là
A. ab = 2
B. ab = 9
C. a = 0
D. a = 3b
Cho hàm số y = a x 2 + b x + c a ≠ 0 có đồ thị (P). Biết đồ thị của hàm số có đỉnh I (1;1) và đi qua điểm A(2;3). Tính tổng S = a 2 + b 2 + c 2 .
A. 3.
B. 4.
C. 29.
D. 1.
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho P: y=ax2+bx+1. Tìm a,b để:
(P) đi qua B(-1;6) và có tung độ đỉnh là -3.
Bài 2:
Ta có: \(\dfrac{-\text{Δ}}{4a}=-3\)
\(\Leftrightarrow-\text{Δ}=-12a\)
\(\Leftrightarrow b^2-4a=12a\)
\(\Leftrightarrow b^2-16a=0\left(1\right)\)
Thay x=-1 và y=6 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+1=6\)
\(\Leftrightarrow a-b=5\)
\(\Leftrightarrow a=b+5\)(2)
Thay (2) vào (1), ta được:
\(b^2-16\left(b+5\right)=0\)
\(\Leftrightarrow b^2-16b+64-144=0\)
\(\Leftrightarrow\left(b-8\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}b=20\\b=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=25\\a=1\end{matrix}\right.\)