Cho đường thẳng d và điểm A không thuộc d. Trên đường thẳng d lấy hai điểm phân biệt B, C (H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng d hay không? Mặt phẳng (ABC) có chứa hai đường thẳng AB và BC hay không?
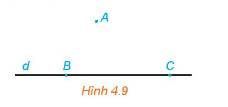
Mặt phẳng (ABC) chứa điểm A và đường thẳng d.
Do đó mp(ABC) cũng chứa hai đường thẳng AB và BC.
Trên mặt phẳng, cho bốn điểm phân biệt A, B, C, D. Liệt kê tất cả các vectơ khác vectơ – không mà điểm đầu và điểm cuối của chúng thuộc tập điểm đã cho.
Cho điểm A không thuộc đường thẳng d. Lấy hai điểm phân biệt B và C thuộc đường thẳng d (Hình 18).
a) Mặt phẳng đi qua ba điểm A, B, C có đi qua đường thẳng d hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm A và đường thẳng d?
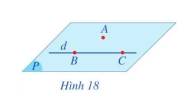
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d
Câu 9: Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 6
B. 4
C. 3
D. 2
Câu 9: Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 6
B. 4
C. 3
D. 2
#HỌC TỐT!
Câu 9: Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 6
B. 4
C. 3
D. 2
Trong mặt phẳng, cho hai đường thẳng song song a và b. Cho 3 điểm phân biệt trên đường thẳng a và 4 điểm phân biệt trên đường thẳng b. Có bao nhiêu tam giác có cả 3 đỉnh là 3 điểm trong 7 điểm nói trên?
Cách 1:
TH1: 2 điểm thuộc a và 1 điểm thuộc b
Số cách chọn 2 điểm thuộc đường thẳng a là \(C_3^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng b là: \(C_4^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_3^2 . C_4^1 = 12\)
TH2: 2 điểm thuộc b và 1 điểm thuộc a
Số cách chọn 2 điểm thuộc đường thẳng b là \(C_4^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng a là: \(C_3^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_4^2 + C_3^1 = 18\)
Vậy có tất cả 12 + 18 = 30 tam giác.
Cách 2:
Số cách chọn 3 điểm thuộc đường thẳng a là: \(C_3^3\) (cách chọn)
Số cách chọn 3 điểm thuộc đường thẳng b là: \(C_4^3\) (cách chọn)
Số cách chọn 3 điểm bất kì trong 7 điểm đã cho là: \(C_7^3\) (cách chọn)
Số cách chọn 3 điểm không thẳng hàng trong 7 điểm đã cho là: \(C_7^3 - C_4^3 - C_3^3 = 30\) (cách chọn)
Vậy số tam giác có thể có là : 30 (tam giác)
Cho đường thẳng d không đi qua O. Trên d lấy sáu điểm A; B; C; D; E; F phân biệt. Có bao nhiêu tam giác nhận điểm O làm đỉnh và hai đỉnh còn lại là hai trong 6 điểm A; B; C; D; E; F
A. 15
B. 12
C. 6
D. 9
Đáp án là A
Số tam giác tạo thành thỏa mãn điều kiện đề bài là: 6(6 - 1)/2 = 15 tam giác.
Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của AB
C. Mặt phẳng song song với đường thẳng AB
D. Trung điểm của đoạn AB
Chọn A.
Gọi I là tâm mặt cầu đi qua hai điểm A, B cố định và phân biệt thì ta luôn có IA = IB. Do đó I thuộc mặt phẳng trung trực của đoạn AB.
Trong các khẳng định sau đây khẳng định nào đúng? khẳng định nào sai?
a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
c) Một mặt phẳng (α) và một đường thẳng a cùng vuông góc với đường thằng b thì a // (α).
d) Hai mặt phẳng (α) và (β) phân biệt cùng vuông góc với một mặt phẳng (γ) thì (α) // (β).
e) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
f) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song.
a) Đúng
b) Đúng
c) Sai
d) Sai
e) Sai
f) Đúng
Quan sát hình vẽ và điền Đ(đúng) hoặc S(sai) và ô vuông
| a. B, C là các điểm nằm trong mặt phẳng (P). | |
| b, Mặt phẳng (P) chứa đựờng thắng AB | |
| c. Đường thẳng l cắt AB ở điểm B | |
| d. A,B,G là ba điểm cùng nằm trên một mặt phẳng | |
| e. B,F và D là ba điểm thẳng hàng | |
| f. B,C,E và D là bốn điểm cùng nằm trên một mặt phẳng |
| a. B, C là các điểm nằm trong mặt phẳng (P). | Đ |
| b, Mặt phẳng (P) chứa đựờng thắng AB | S |
| c. Đường thẳng l cắt AB ở điểm B | S |
| d. A,B,G là ba điểm cùng nằm trên một mặt phẳng | Đ |
| e. B,F và D là ba điểm thẳng hàng | S |
| f. B,C,E và D là bốn điểm cùng nằm trên một mặt phẳng | Đ |
