Tìm số cực trị của hàm số y = x4 + 4x3
A. 1
B. 2
C. 3.
D. 4
Những câu hỏi liên quan
Khi tham số
m
∈
a
;
b
thì hàm số
y
-
x
4
+
4
x
3
-
4
x
2
+
1
-...
Đọc tiếp
Khi tham số m ∈ a ; b thì hàm số y = - x 4 + 4 x 3 - 4 x 2 + 1 - m có số điểm cực trị là lớn nhất. Giá trị a + b bằng
A. 3
B. 0
C. 2
D. 1
Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
Tìm khẳng định đúng trong các khẳng định sau đây:A. Hàm số y
x
3
- 5 có hai cực trị;B. Hàm số y
x
4
/4 + 3
x
2
- 5 luôn đồng biến;C. Tiệm cận ngang của đồ thị hàm số là y -3;D. Đồ thị hàm số sau có hai tiệm cận đứng
Đọc tiếp
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số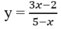 
là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
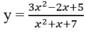
Đáp án: C.
y = -3 là tiệm cận ngang của đồ thị hàm số
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số
m
∈
-
2018
;
2018
để hàm số
y
x
4
-
4
x
3
+
4
x
2
+
m...
Đọc tiếp
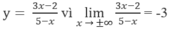
Có bao nhiêu giá trị nguyên của tham số m ∈ - 2018 ; 2018 để hàm số y = x 4 - 4 x 3 + 4 x 2 + m có đúng 5 điểm cực trị.
A. 2019
B. 2020
C. 2017
D. 2018
Chọn đáp án D
Từ bảng biến thiên ta có hàm số có đúng 5 điểm cực trị khi và chỉ khi
Đúng 0
Bình luận (0)
Tìm khẳng định đúng trong các khẳng định sau đây:A. Hàm số y
x
3
- 5 có hai cực trị;B. Hàm số y
x
4
/4 + 3
x
2
- 5 luôn đồng biến;C. Tiệm cận ngang của đồ thị hàm số
y
3
x
-...
Đọc tiếp
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
Đáp án: C.
y = -3 là tiệm cận ngang của đồ thị hàm số
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
+
a
x
2
+
b
. Tìm a, b để hàm số đạt cực trị tại
x
1
và giá trị cực trị bằng
3
2
. A.
a
−
2
b...
Đọc tiếp
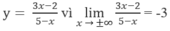
Cho hàm số y = x 4 + a x 2 + b . Tìm a, b để hàm số đạt cực trị tại x = 1 và giá trị cực trị bằng 3 2 .
A. a = − 2 b = 5 2
B. a = 2 b = 5 2
C. a = − 2 b = − 5 2
D. a = 2 b = 2 5
Hàm số y = x 4 - 5 x 2 + 4 có mấy điểm cực đại?
A. 0 B. 2
C. 3 D. 1
Đáp án: D.
Hàm số y = x 4 - 5 x 2 + 4 xác định trên R.
y' = 4 x 3 - 10x = 2x(2 x 5 - 5);
y' = 0 khi
y'' = 12 x 2 - 10
Vì y''(0) = -10 < 0,
nên hàm số chỉ có một cực đại (tại x = 0)
Cách khác: Vì a > 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có một cực đại
Đúng 0
Bình luận (0)
Hàm số y = x 4 - 5 x 2 + 4 có mấy điểm cực đại?
A. 0 B. 2
C. 3 D. 1
Đáp án: D.
Hàm số y = x 4 - 5 x 2 + 4 xác định trên R.
y' = 4 x 3 - 10x = 2x(2 x 2 - 5);
y' = 0 khi
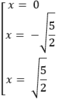
y'' = 12 x 2 - 10
Vì y''(0) = -10 < 0,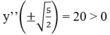
nên hàm số chỉ có một cực đại (tại x = 0)
Cách khác: Vì a > 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có một cực đại
Đúng 0
Bình luận (0)
Cho hàm số y x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại. A.
m
2
±
2
2
B.
m
2
+
2
2
C.
m
2...
Đọc tiếp
Cho hàm số y= x4-2( m+1)x2+ m ( C). Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C có ba điểm cực trị A: B; C sao cho OA= BC ; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có điểm cực trị khi và chỉ khi y’ = 0 có nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)
Khi đó, ta có:
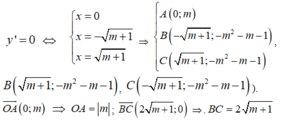
Do đó O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).
Vậy m = 2 ± 2 2 .
Chọn A.
Đúng 0
Bình luận (0)