Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = 2 x 2 + ( 1 - m ) x + 1 + m x - m đồng biến trên khoảng 1 ; + ∞ ?
A. 3.
B. 1.
C. 2.
D. 0.
Hỏi có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = 2 x 2 + ( 1 - m ) x + 1 + m x - m đồng biến trên khoảng ( 1 ; + ∞ ) ?
A. 3.
B. 1.
C. 2.
D. 0.
Cho hàm số f ( x ) = m - 2 x 3 - 2 2 m - 3 x 2 + 5 m - 3 x - 2 m - 2 với m là tham số thực. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x có 5 điểm cực trị?
A. 0.
B. 3.
C. 2.
D. 1.
Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.

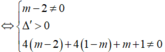
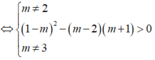
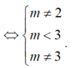

Chọn D
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x - 1 ) 2 ( x 2 - 2 x ) với ∀ x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số có 5 điểm cực trị?
A. 15
B. 17
C. 16
D. 18
Cho hàm số y=f(x) có đạo hàm f’(x)=(x-1)2(x2-2x) với mọi x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm y=f(x2-8x+m) có 5 điểm cực trị
A. 15
B. 17
C. 18
D. 16
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) , với mọi x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 16
B. 18
C. 17
D. 15
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x 2 - 2 x ) với mọi x thuộc R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 15
B. 17
C. 16.
D. 18
Cho hàm số \(y=-2x^3+(2m-1)x^2-(m^2-1)x+2\). Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x = f x 2 + x - 1 + 480 m x 2 + x + 2 nghịch biến trên (0;1)?
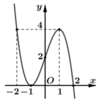
A. 4
B. 6
C. 7
D. 8
Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
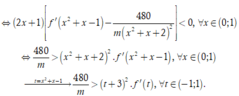
Dựa vào đồ thị, ta có
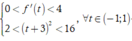
![]()
Theo YCBT 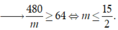
Chọn C.
Cho hàm số y = f x có đạo hàm f ' x = x − 1 2 x 2 − 2 x , với mọi x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x 2 − 8 x + m có 5 điểm cực trị?
A. 16
B. 17
C. 15
D. 18
Đáp án C.
Ta có:
g ' x = 2 x − 8 f ' x 2 − 8 x + m = 0 ⇔ x = 4 f ' x 2 − 8 x + m = 0 ( * ) .
Mà:
f ' x = x − 1 2 x 2 − 2 x = x − 1 2 . x x − 2 ; ∀ x ∈ ℝ .
Suy ra (*)
⇔ x 2 − 8 x + m − 1 2 x 2 − 8 x + m x 2 − 8 x + m − 2 = 0 ⇔ x 2 − 8 x + m − 1 = 0 1 x 2 − 8 x + m = 0 2 x 2 − 8 x + m − 2 = 0 3
Để hàm số đã cho có 5 điểm cực trị khi và chỉ khi:
TH1. (1) có nghiệm kép x = 4 , (2), (3) có 2 nghiệm phân biệt.
TH2. (1) không có nghiệm kép x = 4 , (2), (3) có 2 nghiệm phân biệt.
Khi đó m < 16 là các giá trị thỏa mãn. Kết hợp m ∈ ℤ + ⇒ có 15 giá trị m cần tìm.