Cho hình thang ABCD (AB // CD) có BC = 15cm. Điểm E thuộc cạnh AD sao cho A E A D = 1 3 . Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
A. 15 cm
B. 5 cm
C. 10 cm
D. 7 cm
Những câu hỏi liên quan
Cho hình thang ABCD (AB // CD) có BC = 15cm, AD = 12 cm. Điểm E thuộc cạnh AD sao cho AE = 4. Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
A. 10 cm
B. 5 cm
C. 12 cm
D. 7 cm
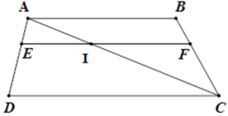
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 4 12 = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B
Đúng 0
Bình luận (0)
Bài 1:cho hình thang vuông ABCD có góc A bằng góc D và bằng 90 độ, AB=12cm, AD=15cm,CD=20cm.tính độ dài cạnh BC.
Bài 2:cho tam giác vuông ABC có góc A bàng 90 độ, điêm D thuộc cạnh AB,điểm E thuộc cạnh Ac. Gọi M,N,P,Q theo thứ tự là trung điểm của DE,BE,BC,CD.CMR:MP=NQ.
Ai làm đc giúp mk vs. Đa tạ.....
Bài 2:
Xét ΔCDB có CQ/CD=CP/CB
nên QP//BD và QP=BD/2
Xét ΔEDB có EM/ED=EN/EB
nên MN//DB và MN=DB/2
=>QP//MN và QP=MN
Xét ΔDEC có DM/DE=DQ/DC
nên MQ//EC và MQ=EC/2
=>MQ vuông góc với AB
=>MQ vuông góc với PQ
=>MNPQ là hình chữ nhật
=>MP=NQ
Đúng 0
Bình luận (0)
Hình thang ABCD (AB//CD) có các tia phân giác góc A và D gặp nhau tại điểm E thuộc cạnh BC. CMR AD= AB+CD
Ta có AB // CD => Góc IDC=Góc DIA ( so le trong )
Mà góc IDC=góc IDA ( do ID là tia phân giác góc ADC)
=> Góc DIA= Góc IDA => tam giác DIA cân tại A
=> AD = AI (1)
Ta có AB // CD => Góc DCI = Góc CIB (so le trong )
Mà góc DCI = góc ICB ( do IC là tia phân giác góc DCB)
=> Góc CIB = Góc ICB => tam giác CIB cân tại B
=> BC = BI (2)
Cộng (1) và (2) , vế theo vế .Ta được:
AD + BC = AI + BI
=> AD + BC = AB (đpcm)
Đúng 0
Bình luận (0)
a)ta có góc BAD+ADC=180 độ (trong cùng phía ABsong song CD)
suy ra (góc BAE+DAE)+(ADE+EDC)=180 độ
2(EAD+ADE)=180 độ
EAD+ADE=90 độ
suy ra AED=90 độ
b)gọi K là giao điểm DE và AB
ta có góc AKE=ADK(cùng bằng với EDC)
suy ra tam giác AKD cân tại A
tam,giác ADK cân tại A có AE là đường cao phân giác
suy ra AE cũng là đường trung trực
vay ED=EK
xét tam giác BEK và CED
ED=EK(cmt)
BEK=CED(đối đỉnh)
BKE=EDC(so le trong ABsong song CD)
vậy tam giác BEK=CED
suy ra CD=NK
vậy AB+BK=AB+CD=AK
mà AK=AD
nên AD=AB+CD
cho hình thang vuông ABCD có A = D = 90độ, AB = AD = CD/2. qua điểm E thuộc cạnh AB, kẻ đường vuông góc với DE, cắt BC tại F. CMR : ED = EF
Dễ thấy \(\widehat{DBC}=90^o\). gọi M là trung điểm của DF.
theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông, ta có :
EM = BM = \(\frac{DF}{2}\)
xét tứ giác MEBF, ta có :
\(\widehat{EBF}=135^o\), \(\widehat{MEB}+\widehat{MFB}=\widehat{MBE}+\widehat{MBF}=\widehat{EBF}=135^o\)
nên \(\widehat{EMF}=360^o-2.135^o=90^o\)
\(\Delta DEF\)có đường cao EM là đường trung tuyến nên ED = EF.
Đúng 0
Bình luận (0)
Hình thang ABCD (AB//CD) có các tia phân giác của các góc A và D gặp nhau tại điểm E thuộc cạnh BC . CMR AD=AB+CD
Ta có AB // CD => Góc IDC=Góc DIA ( so le trong )
Mà góc IDC=góc IDA ( do ID là tia phân giác góc ADC)
=> Góc DIA= Góc IDA => tam giác DIA cân tại A
=> AD = AI (1)
Ta có AB // CD => Góc DCI = Góc CIB (so le trong )
Mà góc DCI = góc ICB ( do IC là tia phân giác góc DCB)
=> Góc CIB = Góc ICB => tam giác CIB cân tại B
=> BC = BI (2)
Cộng (1) và (2) , vế theo vế .Ta được:
AD + BC = AI + BI
=> AD + BC = AB (đpcm)
Đúng 0
Bình luận (0)
gọi K là giao điểm DE và AB
ta có góc AKE=ADK(cùng bằng với EDC)
suy ra tam giác AKD cân tại A
tam,giác ADK cân tại A có AE là đường cao phân giác
suy ra AE cũng là đường trung trực
vay ED=EK
xét tam giác BEK và CED
ED=EK
BEK=CED(đối đỉnh)
BKE=EDC(so le trong ABsong song CD)
vậy tam giác BEK=CED
suy ra CD=NK
vậy AB+BK=AB+CD=AK
mà AK=AD
nên AD=AB+CD
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM AB. Trên tia AB lấy điểm N sao cho AN AC. Chứng minh tứ giác BMCN là hình thangBài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM 1/2 BC, N là trung điểm cạnh AB. Chứng minh:a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA EBBài 4: Cho ABCD là hình thang ( AB // CD, AB CD...
Đọc tiếp
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM = AB. Trên tia AB lấy điểm N sao cho AN = AC. Chứng minh tứ giác BMCN là hình thang
Bài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM= 1/2 BC, N là trung điểm cạnh AB. Chứng minh:
a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông
Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD = góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA = EB
Bài 4: Cho ABCD là hình thang ( AB // CD, AB < CD ). Kẻ các đường cao AE,BF của hình thang. C/minh rằng DE = CF
Bài 5: Cho ABCD là hình thang ( AB // CD ) có DB là đường phân giác góc D và AE là đường phân giác góc A ( E thuộc DC ). Biết AE // BC và O là giao điểm của AE với DB. CMR:
a) AE vuông góc với DB
b) AD // BE và AD = BE
c) E là trung điểm của DC
d) Xác định dạng của tứ giác BCEO
e) Biết góc BEC = 80 độ. Hãy tính các góc của hình thang ABCD
Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
Đúng 0
Bình luận (0)
cho hình thang abcd ,có e và m là 2 điểm thuộc cạnh ad sao cho am=me=ed,có n và f là 2 điểm thuộc cạnh bc sao cho bn=nc=fc,biết ab-3,cd=15.tính độ dài mn và ef
Cho hình thang ABCD có A=D=90 độ, AB=10cm, CD=30cm, AD=35cm, điểm E thuộc AD sao cho AE=15cm. Tính góc BEC
Cho hình thang vuông ABCD có góc A = góc D = 90 độ, AB = AD = CD/2. Qua điểm E thuộc cạnh AB,kẻ đường vuông góc với DE cắt BC tại F. Chứng minh: ED = EF.