Cho hình vẽ bên. Có bao nhiêu cặp tam giác vuông đồng dạng với nhau là:
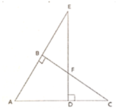
A. 3
B. 4
C. 5
D. 6
Cho hình bên là tam giác ABC vuông tại A, đường cao AH. Trong hình bên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.
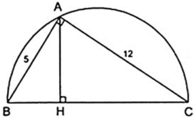
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.
Câu 4:
4.1 Cho AABC vuông tại A và có dưong cao AH. a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau ? (Viết từng cặp tam giác đồng dạng theo thứ tự các đinh tương ứng) b) Biết AB= 6cm, AC = 8cm. Tính độ dài các đoạn thắng BC, AH, BH. c) Chứng minh: HB.HC = HA.
4.2 Cho hình chữ nhật ABCD có AB = a =12cm, BC b = 9cm. Gọi H là chân dưong vuông góc kẻ từ A xuống BD. a. Chứng minh AAHB đồng dạng ABCD. b. Tính độ dài đoạn AH. c. Tính diện tích tam giác AHB.
4.3. Cho tam giác ABC vuông tại A, AB= 9cm, AC= 12cm. Tia phân giác của góc A cắt BC tại D. Từ D kẻ DE AC tại E. A ABC. al Chứng minh AEDC 5/ Chứng minh AC.ED AB.EC; c/ Tính độ dài các đoạn CD, CE
4.2:
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH=góc BDC
=>ΔAHB đồng dạng với ΔBCD
b: BD=căn 9^2+12^2=15cm
AH=9*12/15=108/15=7,2cm
c: HB=AB^2/BD=12^2/15=9,6cm
S AHB=1/2*AH*HB=1/2*7,2*9,6=34,56cm2
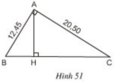
Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.
a) ΔABC 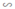 ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC 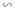 ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA 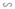 ΔHAC vì cùng đồng dạng với ΔABC.
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)

Ở hình 51, tam giác ABC vuông ở A và có đường cao AH
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau ? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng)
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH, CH ?
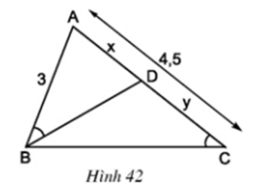
Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và ∠(ABD) = ∠(BCA).
a) Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?
b) Hãy tính các độ dài x và y (AD = x, DC = y).
c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
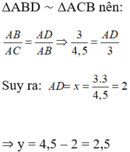
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
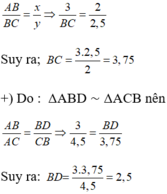
Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và ∠(ABD) = ∠(BCA).
a) Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?
b) Hãy tính các độ dài x và y (AD = x, DC = y).
c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
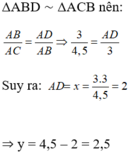
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
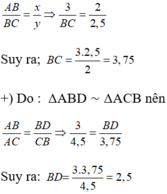
Bài 4. Cho tam giác DEF vuông tại D có DE = 9cm DF = 12cm Tia phân giác của góc D cắt EF tại P. Từ P kẻ PH vuông góc DF (H thuộc DF). a) Tính tỉ số (EP)/(FP) b) Tìm các cặp tam giác đồng dạng có trong hình vẽ và tỉ số đồng dạng. c) Tính PH.
a: EP/FP=DE/DF=3/4
b: Xet ΔFHP vuông tại H và ΔFDE vuông tại D có
góc HFP chung
=>ΔFHP đồng dạng vơi ΔFDE
c: ΔFHP đồng dạng với ΔFDE
=>HP/DE=FP/FE=4/7
=>HP/9=4/7
=>HP=36/7(cm)
a: EP/FP=DE/DF=3/4
b: Xet ΔFHP vuông tại H và ΔFDE vuông tại D có
góc HFP chung
=>ΔFHP đồng dạng vơi ΔFDE
c: ΔFHP đồng dạng với ΔFDE
=>HP/DE=FP/FE=4/7
=>HP/9=4/7
=>HP=36/7(cm)
Hình bs.5 cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H
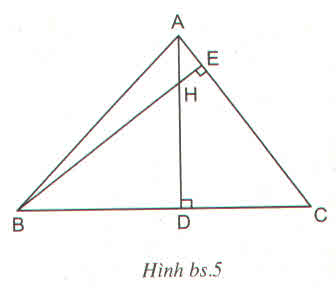
Trong hình bs.5 có số cặp tam giác đồng dạng với nhau là :
(A) 1 cặp
(B) 2 cặp
(C) 3 cặp
(D) 4 cặp
Hãy chọn kết quả đúng ?
Trên hình bs 6 , có bao nhiêu cặp tam giác bằng nhau ?
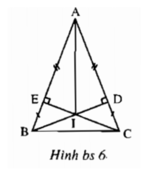
(A) 2; (B) 3; (C) 4 (D) 5;
Hãy chọn đáp án đúng
Chọn D. Năm cặp tam giác bằng nhau là:
ΔAEI = ΔADI, ΔBEI = ΔCDI, ΔAIB = ΔAIC, ΔBEC = ΔCDE, ΔABD = ΔACE.