Cho khối chóp S.ABC có SA = 3, SB = 4, SC = 5, A S B ^ = B S C ^ = C S A ^ = 60 ° . Thể tích khối chóp S.ABC bằng:
A. 5 2
B. 5 3
C. 10
D. 15
Cho hình chóp S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA = 3, SB = 4, SC 5, thể tích khối chóp S.ABC bằng
A. 20.
B. 30.
C. 10.
D. 60.
Phương pháp:
Thể tích tứ diện vuông là V = 1 6 abc
Cách giải:
Thể tích ![]()
Chọn C.
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.
A. V = 1 6 a b c
B. V = 1 3 a b c
C. V = a b c
D. V = 1 2 a b c
Đáp án A
Phương pháp:
Thể tích khối chóp vuông
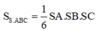
Cách giải:
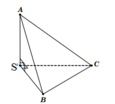
S.ABC có SA, SB, SC đôi một vuông góc với nhau
⇒ S.ABC là tứ diện vuông tại đỉnh S

Cho khối chóp S . A B C có S A , S B , S C đôi một vuông góc với nhau và S A = a , S B = b , S C = c . Tính thể tích khối chóp S . A B C .
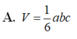
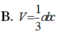
![]()
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC .
A. V = 1 6 a b c
B. V = 1 3 a b c
C. V = abc
D. V = 1 2 a b c
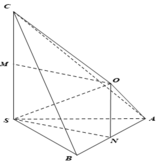
Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:
A. 25 2 π
B. 125 2 π 3
C. 10 2 π 3
D. 5 2 π 3 3
Đáp án B
Gọi M,N lần lượt là trung điểm SC, AB
Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .
Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)

Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:
A. 25 2 π
B. 125 2 π 3
C. 10 2 π 3
D. 5 2 π 3 3
Cho khối chóp S.ABC có các điểm A', B', C' lần lượt thuộc các cạnh SA, SB, SC thỏa 3SA' = SA, 4SB' = SB, 5SC' = 3SC. Biết thể tích khối chóp S.A'B'C' bằng 5 ( c m 3 ). Tìm thể tích khối chóp S.ABC
A. 120 ( c m 3 )
B. 60 ( c m 3 )
C. 80 ( c m 3 )
D. 100 ( c m 3 )
Đáp án D
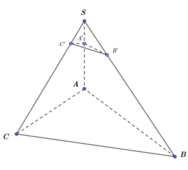
Key: Tính thể tích khối chóp B’.SA’C’ ta có:
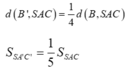
Suy ra:
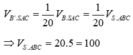
=> Chọn đáp án D.
Cho khối chóp S.ABC có SA = 9, SB = 4, SC = 8 và đôi một vuông góc. Các điểm A', B', C' thỏa mãn SA→ = 2SA'→, SB→ = 3SB'→, SC→ = 4SC'→. Thể tích khối chóp S.A'B'C' là:
A. 24
B. 16
C. 2
D. 12
Cho khối chóp S.ABC. Trên các đoạn SA. SB, SC lần lượt lấy ba điểm A', B'. C' sao cho SA' = 1 2 SA, SB' = 1 3 SB, SC' = 1 4 SC. Khi đó tỉ số thể tích của hai khối chóp S.A'B'C' và S.ABC bằng
A. 1 2
B. 1 12
C. 1 24
D. 1 6