Phương pháp:
Thể tích tứ diện vuông là V = 1 6 abc
Cách giải:
Thể tích ![]()
Chọn C.
Phương pháp:
Thể tích tứ diện vuông là V = 1 6 abc
Cách giải:
Thể tích ![]()
Chọn C.
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.
A. V = 1 6 a b c
B. V = 1 3 a b c
C. V = a b c
D. V = 1 2 a b c
Cho khối chóp S . A B C có S A , S B , S C đôi một vuông góc với nhau và S A = a , S B = b , S C = c . Tính thể tích khối chóp S . A B C .
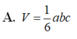
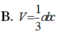
![]()
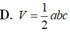
Khối chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau, S A = a , S B = 3 a , . Thể tích khối chóp S.ABC tính theo a là
A. a 3
B. 4 a 3
C. 12 a 3
D. 2 a 3
Cho khối chóp S.ABC có ba cạnh SA, SB, SC cùng độ dài bằng a và vuông góc với nhau từng đôi một. Thể tích của khối chóp S.ABC bằng
A. a 3 6
B. a 3
C. a 3 2
D. a 3 3
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng a 3 6 . Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
A. r = a 3 + 3
B. r = 2a
C. r = a 3 3 + 2 3
D. r = 2 a 3 3 + 2 3
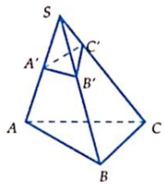
Cho khối chóp S.ABC có SA = 9, SB = 4, SC = 8 và đôi một vuông góc. Các điểm A', B', C' thỏa mãn SA→ = 2SA'→, SB→ = 3SB'→, SC→ = 4SC'→. Thể tích khối chóp S.A'B'C' là:
A. 24
B. 16
C. 2
D. 12
Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:
A. 25 2 π
B. 125 2 π 3
C. 10 2 π 3
D. 5 2 π 3 3
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Tính thể tích của khối chóp S. ABC.
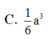
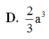
Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt phẳng qua A vuông góc với SC cắt SB, SC lần lượt tại M, N. Biết rằng SA = AC = 5, AB = 3, BC = 4. Thể tích khối chóp S.AMN bằng:
A. 125 68 B. 125 34
C. 175 34 D. 125 17