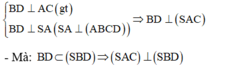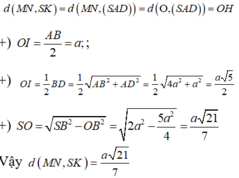Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).

Những câu hỏi liên quan
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính \(\cos\widehat{MAN}\) ?
Cho hình vuông ABCD . gọi M ,N lần lượt là trung điểm của BC và CD. Tính cos góc MAN
Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)
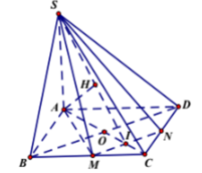
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Tính góc giữa SM và (ABCD).
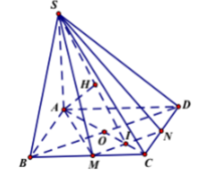
AM là hình chiếu của SM trên (ABCD).
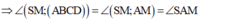
- Xét tam giác vuông ABM ta có: 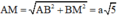
- Xét tam giác vuông SAM ta có: 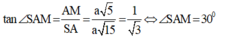
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Tính khoảng cách từ điểm C đến mặt phẳng (SMN)?
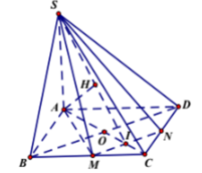
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
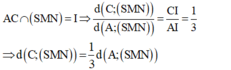
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
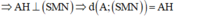
- Ta có:
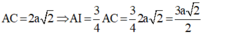
- Xét tam giác vuông SAI ta có:
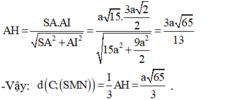
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và S A = a 15 Gọi M, N lần lượt là trung điểm của BC và CD: Chứng minh (SAC) ⊥ (SBD).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB2a, BCa. Các cạnh bên của hình chóp bằng nhau và bằng
a
2
. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
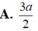
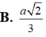
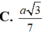
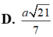
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB2a, BCa. Các cạnh bên của hình chóp bằng nhau và bằng
a
2
. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD2KA. Tính khoảng cách giữa hai đường thẳng MN và SK. A.
3
a
2
B.
a
2
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
A. 3 a 2
B. a 2 3
C. a 3 7
D. a 21 7
Đáp án D
Phương pháp:
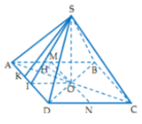
- Tìm một mặt phẳng chứa SK mà song song với MN, đó chính là mặt phẳng (SAD)
- Từ đó ta chỉ cần tính khoảng cách từ MN đến (SAD).
Cách giải: Gọi I là trung điểm AD, AC cắt BD tại O. H là hình chiếu vuông góc của O trên SI.
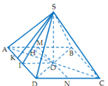
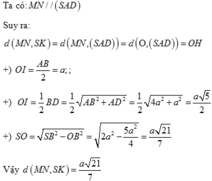
Chú ý khi giải: HS thường không chú ý đến phương pháp tìm mặt phẳng song song mà chỉ tập trung đi tìm đường vuông góc chung dẫn đến sự phức tạp cho bài toán và không đi đến được đáp án.
Đúng 0
Bình luận (0)
cho hình vuông ABCD có cạnh bằng 8cm. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Hãy tìm diện tích của hình vuông MNPQ.
cho hình vuông ABCD có cạnh bằng a. các điểm M,N nằm trên các cạnh BC, CD ( M khác B,M khác C,N khác C,N khác D) sao cho góc MAN45 độ. gọi E,F lần lượt là giao điểm của AM, AN trên BDa) chứng minh chu vi tam giác MNC2ab) chứng minh rằng MF vuông góc với ANC) tính diện tích tam giác AMN khi M,N lần lượt là giao điểm của tia phân giác của góc BAC với cạnh BC; tia phân giác của góc DAC với cạnh CD và a4cm
Đọc tiếp
cho hình vuông ABCD có cạnh bằng a. các điểm M,N nằm trên các cạnh BC, CD ( M khác B,M khác C,N khác C,N khác D) sao cho góc MAN=45 độ. gọi E,F lần lượt là giao điểm của AM, AN trên BD
a) chứng minh chu vi tam giác MNC=2a
b) chứng minh rằng MF vuông góc với AN
C) tính diện tích tam giác AMN khi M,N lần lượt là giao điểm của tia phân giác của góc BAC với cạnh BC; tia phân giác của góc DAC với cạnh CD và a=4cm