Lời giải:

$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$

$=(2a+b)^2-6(2a+b)+3b^2-6b+12$

$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$

$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$

Vậy $P_{\min}=0$

Giá trị này đạt tại $2a+b-3=b-1=0$

$\Rightarrow b=1; a=1$

Lời giải:

$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$

$=(2a+b)^2-6(2a+b)+3b^2-6b+12$

$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$

$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$

Vậy $P_{\min}=0$

Giá trị này đạt tại $2a+b-3=b-1=0$

$\Rightarrow b=1; a=1$

\(P=4a^2+4ab+4b^2+-12a-12b+12\)

\(=\left(\left(2a^2+4ab+2b^2\right)-8\left(a+b\right)+8\right)+\left(2a^2-4a+2\right)+\left(2b^2-4b+2\right)\)

\(=2\left(a+b-2\right)^2+2\left(a-1\right)^2+2\left(b-1\right)^2\ge0\)

Vậy GTNN của P = 0 khi x = y = 1

P = 4a² + 4ab + 4b² - 12a - 12b + 12

= [(4a² - 12a + 9) + (4ab - 6b) + b²] + (3b² - 6b + 3)

= [(2a - 3)² + 2b(2a - 3) + b²] + 3(b - 1)²

= (2a + b - 3)² + 3(b - 1)²\(\ge0\)

Dấu = xảy ra khi a = b = 1

Đáp án đúng : A

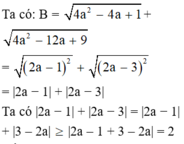
Dấu “=” xảy ra  ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2

Vậy GTNN của B là 2 khi  1 2 ≤ a ≤ 3 2

$P=4a^2+4a(b-3)+b^2-6b+9+3b^2-6b+3$

$=4a^2+2.2a.(b-3)+(b-3)^2+3.(b-1)^2$

$=(2a+b-3)^2+3.(b-1)^2$

Mà $(2a+b-3)^2 \geq 0;3.(b-1)^2 \geq 0$ với mọi $a;b$

Nên $P=(2a+b-3)^2+3.(b-1)^2 \geq 0$

Dấu $=$ xảy ra $⇔(2a+b-3)^2=0;3.(b-1)^2=0⇔2a+b-3=0;b=1⇔a=1;b=1$

Vậy $MinP=0$ tại $a=b=1$

A= 4a^2 + 4ab + 4b^2 - 12a - 12b + 12 
=(2a+2b-3)^2 + 3 
=>minA = 3

Ta có:

P=4a²+4ab+4b²-12a-12b+12

  =[(4a²-12a+9)+2b(2a-3)+b²]+3b²-6b+12

  =(2a+b-3)²+3(b-1)²+9    

Dấu "=" xảy ra khi 2a+b-3=0 và b-1=0

                       <=>2a+1-3=0 và  b=1

                       <=>a=1 và b=1

Vậy MinP=9 <=> a=b=1

Minh Lê Thái Bình xem lại cách giải nha :))))))))

Cả Lê Minh và Hà Nguyễn đều giải sai. Min P = 0 khi a = b = 1 mới đúng. Mình test rồi.

2a=x

2b=y

cho gọn hệ số

\(\Leftrightarrow x^2+xy+y^2-6x-6y+12\\ \\\)

\(\left(x+\frac{y}{2}-3\right)^2+\left(y^2-6y+12\right)-\left(\frac{y^2}{4}-3y+9\right)\) để nguyên lại cho bạn dẽ hiểu

\(\left(x+\frac{y}{2}-3\right)^2+\frac{3}{4}\left(y-2\right)^2\ge0\)đẳng thức khi y=2; x=2=> a=b=4

Bác Ngô Như Minh giải đúng rồi. Nhầm một tí ở đoạn cuối cùng, đó là a = b = 1 mới đúng.

Tuy nhiên chỗ đó không quan trọng lắm. Nhầm lẫn là chuyện bình thường.

Ủng hộ bác Minh vác Kiếm tung hoành thiên hạ. Em chọn đúng rồi đấy.

uh chuẩn toán học nhầm , sai là chuyện bt mà "đb là cộng trừ nhân chia).

mình rất muốn có người chi ra cái sai bài làm của mình (đb là phần lập luận)

a)1200

b)240

a) 12a + 12b = 12.20 + 12.80

                   = 12.( 20 + 80 )

                   = 12.100 = 1200

b) 12a + 12b = 12.( a + b)

                   =  12 .20

                   = 240

a)12.20+12.80

 =240+960

 =1200

b)12.a+12.b

 =12.(a+b)

 =12.20

 =240