Đáp án B

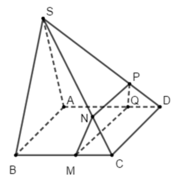
Ta có: MN // BS ⇒ C M C B = C N C S

MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A

NP // CD ⇒ C N C S = D P D S

Do đó: D P D S = D Q D A  PQ // SA (Định lý Ta - lét trong tam giác SAD)

Lại có MN // BS và SB ∩  SA = S

Do đó MN không thể song song với PQ

Xét tứ giác MNPQ có NP // MQ (//CD)

Do đó MNPQ là hình thang.

Vậy khẳng địn (1) và (3) đúng.

Đáp án B

1: Xét ΔNMP có NA/NM=NB/NP

nên AB//MP và AB=MP/2

Xét ΔQMP có QC/QP=QD/QM

nên DC//MP và DC=MP/2

=>AB//DC và AB=DC

=>ABCD là hình bình hành

e lam ho bai a+b+ab=3 tim gtnn a^2+b^2

xét tg MNQ

MA=AN

QD=DM

=>AD là đường tb tg ABC

=>AD=NQ/2,AD//NQ(1)

xét tg PNQ

BP=BN

QC=CP

=>BC là đường tb tg PNQ

=>BC=NQ/2,BC//NQ(2)

Từ (1)(2)

=> ABCD hình bình hành 

vẽ hình bạn nhớ kẻ thêm đường chéo AC

a: Xét ΔMNP và ΔPQM có

MN=PQ

NP=QM

MP chung

=>ΔMNP=ΔPQM

b: Xét tứ giác MNPQ có

MQ=NP

MN=PQ

=>MNPQ là hình bình hành

=>MN//PQ và MQ//NP

tự vẽ hình

nối MP

Xét t/g MNP có: AM=AN(gt),BN=BP(gt)

=>AB là đường tb của t/g MNP

=>AB//MP và  AB=1/2MP (1)

Xét t/g MQP có: MD=DQ(gt),QC=CP(gt)

=>CD là đường tb của t/g MQP

=.CD//MP và  CD=1/2MP(2)

Từ  (1) và  (2) => AB=CD (3)

Lại có:AB//MP, CD//MP

=>AB//CD (4)

Từ (3)và (4) => tứ giác ABCD là HBH

xét tứ giác MABQ

MA//BQ,MA=BQ

=>MABQ hình bình hành

MN//PQ (cạnh đối hbh) => MI//KQ

Ta có

\(MI=\dfrac{MN}{2};KQ=\dfrac{PQ}{2}\) Mà MN=PQ (cạnh đối hbh) => MI=KQ

=> MIKQ là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

b/

Ta có

MA=MQ (gt) (1)

\(MN=2MQ\left(gt\right)\Rightarrow MQ=\dfrac{MN}{2}\) (2)

Ta có

\(MI=\dfrac{MN}{2}\) (3)

Từ (1) (2) (3) \(\Rightarrow MA=MI=\dfrac{MN}{2}\) => tg AMI cân tại M

Ta có

\(\widehat{AMI}=\widehat{AMP}-\widehat{M}=180^o-120^o=60^o\)

Xét tg AMI có

\(\widehat{MAI}+\widehat{MIA}+\widehat{AMI}=180^o\)

\(\Rightarrow\widehat{MAI}+\widehat{MIA}=180^o-\widehat{AMI}=180^o-60^o=120^o\)

Mà \(\widehat{MAI}=\widehat{MIA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\dfrac{120^o}{2}=60^o\)

\(\Rightarrow\widehat{MAI}=\widehat{MIA}=\widehat{AMI}=60^o\Rightarrow\Delta AMI\) là tg đều

c/

Xét hbh MNPQ có

MQ//NP => MA//NP

MA=MQ (gt); MQ=NP (cạnh đối hbh)

=> MA=NP

=> APMN là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Ta có

\(MI=AI=\dfrac{MN}{2}\)  (cạnh tg đều)

\(NI=\dfrac{MN}{2}\)

\(\Rightarrow AI=NI=\dfrac{MN}{2}\) => tg AIN cân tại I

Ta có \(\widehat{AIN}=\widehat{MIN}-\widehat{AIM}=180^o-60^o=120^o\)

Xét tg cân AIN có

\(\widehat{AIN}+\widehat{IAN}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{IAN}+\widehat{INA}=180^o-\widehat{AIN}=180^o-120^o=60^o\)

Mà \(\widehat{IAN}=\widehat{INA}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{IAN}=\widehat{INA}=\dfrac{60^o}{2}=30^o\)

Xét tg AMN có

\(\widehat{MAN}+\widehat{AMI}+\widehat{INA}=180^o\)

\(\Rightarrow\widehat{MAN}=180^o-\widehat{AMI}-\widehat{INA}=180^o-60^o-30^o=90^o\)

=> APMN là hình chữ nhật (hình bình hành có 1 góc vuông là HCN

Tham khảo nhé