Hàm số y = 2cos2 x + 3cos3x + 8cos4x tuần hoàn với chu kì
A. π
B. 2π
C. 3π
D. 4π
Những câu hỏi liên quan
Hàm số y = sin ( π / 2 - x ) + c o t x / 3 là hàm tuần hoàn với chu kì:
A. T = π.
B. T = 2π.
C. T = 3π.
D. T = 6π.
Hàm số y 1 = sin π 2 − x có chu kì T 1 = 2 π − 1 = 2 π
Hàm số y 2 = cot x 3 có chu kì T 2 = π 1 3 = 3 π
Suy ra hàm số đã cho y = y 1 + y 2 có chu kì T = B C N N 2 , 3 π = 6 π .
Vậy đáp án là D.
Đúng 0
Bình luận (0)
Trong các hàm số sau, hàm số nào tuần hoàn với chu kì 2 π ?
A. y = cos2x
B. y = sinx
C. y = tanx
D. y = cotx
Trong các hàm số sau, hàm số nào tuần hoàn với chu kì 2 π ?
A. y = cos 2x
B. y = sinx
C. y = tanx
D. y = cotx
Đáp án B.
Các hàm cos 2x, tan x, cot x có chu kì π .
Đúng 0
Bình luận (0)
Hàm số nào sau đây tuần hoàn với chu kì
T
2
π
? A.
y
tan
2
x
B.
y
sin
2
x
+
cos
3
x
C.
y
sin
x
2
−
cos
2
x
D.
y
cos...
Đọc tiếp
Hàm số nào sau đây tuần hoàn với chu kì T = 2 π ?
A. y = tan 2 x
B. y = sin 2 x + cos 3 x
C. y = sin x 2 − cos 2 x
D. y = cos 2 x + 1
Cho hình trụ có bán kính đáy a và có thiết diện qua trục là một hình vuông. Diện tích xung quanh của hình trụ là:A. 3π
a
2
B. 2π
a
2
C. 4π
a
2
D. π
a
2
Đọc tiếp
Cho hình trụ có bán kính đáy a và có thiết diện qua trục là một hình vuông. Diện tích xung quanh của hình trụ là:
A. 3π a 2 B. 2π a 2
C. 4π a 2 D. π a 2
Chọn C.
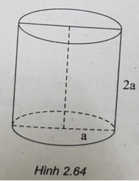
(h.2.63) Một hình trụ có bán kính đáy a, có thiết diện qua trục là một hình vuông nên chiều cao hình trụ bằng 2a.
Vậy diện tích xung quanh khối trụ là:
S xq = 2 πRh = 4 πa 2
Đúng 0
Bình luận (0)
Cho các mệnh đề sau(I) Hàm số
f
x
sin
x
x
2
+
1
là hàm số chẵn.(II) Hàm số
f
x
3
sin
x
+
4
cos
x
có giá trị lớn nhất là 5.(III) Hàm số
f...
Đọc tiếp
Cho các mệnh đề sau
(I) Hàm số f x = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f x = 3 sin x + 4 cos x có giá trị lớn nhất là 5.
(III) Hàm số f x = tan x tuần hoàn với chu kì 2 π .
(IV) Hàm số f x = cos x đồng biến trên khoảng 0 ; π .
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4.
B. 2.
C. 3.
D. 1.
tính giá trị biểu thức
sin(x+π/5) sin(x+2π/5)+sin (x+3π/5) + sin(x+4π/5)
Cho các mệnh đề sau (I) Hàm số
f
x
sin
x
x
2
+
1
là hàm số chẵn. (II) Hàm số
f
x
3
sin
x
+
4
cos
x
có giá trị lớn nhất là 5. (III) Hàm số
f
x
tan...
Đọc tiếp
Cho các mệnh đề sau
(I) Hàm số f x = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f x = 3 sin x + 4 cos x có giá trị lớn nhất là 5.
(III) Hàm số f x = tan x tuần hoàn với chu kì 2 π .
(IV) Hàm số f x = cos x đồng biến trên khoảng 0 ; π .
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4
B. 2
C. 3
D. 1
Tổng các nghiệm thuộc đoạn [0; 3π] của phương trình 1 - 2 cos^2 x - sin x = 0 là
A. 5/3π. B. 4π. C. 6π. D. 7/2π .
\(1-2cos^2x-sinx=0\)
\(\Leftrightarrow1-2\left(1-sin^2x\right)-sinx=0\)
\(\Leftrightarrow2sin^2x-sinx-1=0\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{2};\dfrac{7\pi}{6};\dfrac{11\pi}{6};\dfrac{5\pi}{2}\right\}\)
\(\Rightarrow\sum x=6\pi\)
Đúng 1
Bình luận (0)