Cho hình chóp S. ABC có AB=AC, S A C ^ = S A B ^ . Tính số đo của góc giữa hai đường thẳng SA và BC
A. 45 °
B. 60 °
C. 30 °
D. 90 °
Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC). Tam giác ABC vuông tại C, AB = a 3 , AC=a. Tính thể tích khối chóp S. ABC biết rằng SC = a 5 .
A. a 3 6 6
B. a 3 6 4
C. a 3 2 3
D. a 3 10 6
Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = a 3 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm của cạnh AC. Biết SB = a 2 Tính theo a khoảng cách từ H đến mặt phẳng (SAB)
A. 7 a 21 3
B. a 21 7
C. a 21 3
D. 3 a 21 7
Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SAC vuông cân tại S. Biết AB=a, AC=2a, S A C ⊥ A B C . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
A. 2 πa 2
B. 4 πa 2
C. 5 πa 2
D. 3 πa 2
Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SAC vuông cân tại S. Biết AB = a, Ac = 2a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
A. 2 π a 2
B. 4 π a 2
C. 5 π a 2
D. 3 π a 2
Chọn C.
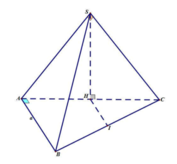
Gọi H, I lần lượt là trung điểm của BC, AC.
Tam giác SAC vuông cân tại S
Tam giác ABC vuông tại A => IA= IB = IC (1).
Lại có:
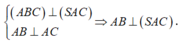
Mà HI là đường trung bình của tam giác ABC
![]()
![]()
![]()
Do đó: I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
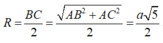
Vậy diện tích mặt cầu là
![]()
Cho khối chóp S.ABC có S A ⊥ ( A B C ) , SA=a, AB=a, AC=2a. Tính thể tích khối chóp S. ABC.
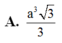
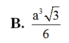
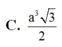
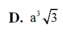
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, A B = a ; A C = a 2 Biết thể tích khối chóp này bằng a 3 2 Khoảng cách từ điểm S đến mặt phẳng (ABC) bằng
A. 3 a 2
B. a 2
C. 3a/2
D. a/2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Tính thể tích khối chóp S.ABC biết AB = a, AC = a 3 , SB = a 2 .
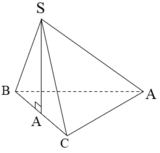
A. a 3 6 6
B. a 3 3 2
C. a 3 3 6
D. a 3 6 2
Hình chóp A'.BC'D có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA = a, AB = b, AC = c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ?
A. R = 2 ( a + b + c ) 3
B. R = 2 a 2 + b 2 + c 2
C. R = 1 2 a 2 + b 2 + c 2
D. R = a 2 + b 2 + c 2
Đáp án C
Hướng dẫn giải:
Gọi H, K lần lượt là trung điểm của BC và SA.
Dựng đường thẳng d đi qua H và vuông góc với (ABC). Khi đó d//SA.
Trong mặt phẳng (SAH) dựng đường thằng d 1 đi qua K và vuông góc với SA.
Khi đó, d 1 //AH.
Gọi I = d ∩ d 1 tại. Ta có được IA = IB = IC = IS.
Khi đó mặt cầu cần tìm ở đề bài đi qua các điểm A, B, C, S có tâm là I và bán kính là R = IA.
Dễ thấy A H = 1 2 B C = b 2 + c 2 2
và I H = 1 2 S A = a 2 .
Trong ∆ I A H có
![]()
Vậy là ta hoàn thành xong bài toán.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Tính thể tích khối chóp S.ABC biết A B = a , A C = a 3 , S B = a 2
A. a 3 6 6
B. a 3 3 2
C. a 3 3 6
D. a 3 6 2