Cho hình chóp S.ABC có cạnh SA vuông góc với mặt phẳng biết A B = A C = a , B C = a 3 . Tính góc giữa hai mặt phẳng (SAB) và (SAC).
A. 30 °
B. 150 °
C. 60 °
D. 120 °
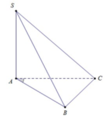
Đáp án C
Ta có S A ⊥ B A C ⇒ S A B ; S A C ⏜ = B A C ⏜ hoặc 180 ° − B A C ⏜
Lại có cos B A C ⏜ = A B 2 + A C 2 − B C 2 2 A B . A C = − 1 2 ⇒ B A C ⏜ = 120 °
Vậy S A B ; S A C ⏜ = 60 °
Cho hình chóp S.ABC có AB=2a,BC=a, A B C ^ = 120 0 . Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC),d(C,SA)=2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng
A. 777 37
B. 4 37 37
C. 21 10
D. 10 11
Cho hình chóp S.ABC có AB=2a, BC = a, A B C ^ = 120 o Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), d(C,SA)=2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng
A. 777 37
B. 4 37 37
C. 21 10
D. 10 11 .
Cho hình chóp S. ABC có cạnh SA vuông góc với mặt phẳng (ABC) biết AB = AC =a, BC= a 3 . Tính góc giữa hai mặt phẳng (SAB) và (SAC).
A. 30 0
B. 150 0
C. 60 0
D. 120 0
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB=2a,AC=a và SA vuông góc với mặt phẳng (ABC). Biết góc giữa hai mặt phẳng (SAB) và (SBC) bằng 60°. Tính thể tích khối chóp S.ABC.
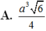
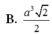
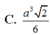
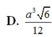
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB=2a, AC=a và SA vuông góc với mặt phẳng (ABC). Biết góc giữa hai mặt phẳng (SAB) và (SBC) bằng 60°. Tính thể tích khối chóp S.ABC.
A. a 3 6 4
B. a 3 2 2
C. a 3 2 6
D. a 3 6 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, B C = 2 a ; cạnh bên SA vuông góc với mặt đáy. Biết rằng số đo của góc giữa hai mặt phẳng (ABC) và (ABC) bằng 60 0 . Khoảng cách từ trọng tâm G của tam giác SAB đến mặt phẳng (SAC) bằng
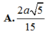
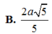
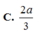
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a; cạnh bên SA vuông góc với mặt đáy. Biết rằng số đo của góc giữa hai mặt phẳng (ABC) và (ABC) bằng 60 ° . Khoảng cách từ trọng tâm G của tam giác SAB đến mặt phẳng (SAC) bằng
A. 2 a 5 15
B. 2 a 5 5
C. 2 a 3
D. a 3
Cho hình chóp S.ABC có SC vuông góc với (ABC) và tam giác ABC vuông tại B. Biết AB=a, AC=a√3, SC=2a√6. Sin của góc giữa hai mặt phẳng (SAB); (SAC) bằng
Qua C kẻ đường thẳng vuông góc AC cắt AB kéo dài tại D
\(\left\{{}\begin{matrix}SC\perp\left(ABC\right)\Rightarrow SC\perp CD\\CD\perp AC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAC\right)\)
Kẻ \(CH\perp SB\Rightarrow CH\perp\left(SAB\right)\)
\(\Rightarrow\widehat{HCD}\) là góc giữa (SAB) và (SAC)
\(BC=\sqrt{AC^2-AB^2}=a\sqrt{2}\)
\(\dfrac{1}{CH^2}=\dfrac{1}{SC^2}+\dfrac{1}{BC^2}=\dfrac{13}{24a^2}\Rightarrow CH=\dfrac{2a\sqrt{78}}{13}\)
\(CD=AC.tanA=AC.\dfrac{BC}{AB}=a\sqrt{6}\)
\(sin\widehat{HCD}=\dfrac{DH}{CD}=\dfrac{\sqrt{CD^2-CH^2}}{CD}=...\)
