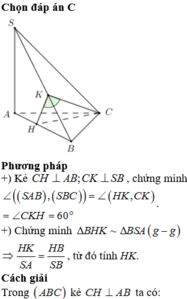
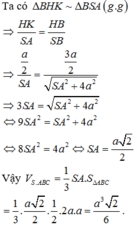Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC), tính
cos
α
khi thể tích khối chóp
S
.
A
B
C
nhỏ nhất. A.
cos
α
2
2
B.
cos
α
1
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC), tính cos α khi thể tích khối chóp S . A B C nhỏ nhất.
A. cos α = 2 2
B. cos α = 1 3
C. cos α = 3 3
D. cos α = 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với ABa và BAC
30
°
Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC) Tính khoảng cách d từ điểm A đến mặt phẳng (SBC) biết khối chóp S.ABC có thể tích bằng
a
3
3
36
A.
d
a
2
4...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với AB=a và BAC= 30 ° Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABC) Tính khoảng cách d từ điểm A đến mặt phẳng (SBC) biết khối chóp S.ABC có thể tích bằng a 3 3 36
A. d = a 2 4
B. d = a 3
C. d = a 5 3
D. d = a 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy ABC, góc giữa hai mặt phẳng
S
B
C
và
A
B
C
bằng 60°. Tính thể tích V của khối chóp S.ABC. A.
a
3
3
8
B.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với đáy ABC, góc giữa hai mặt phẳng S B C và A B C bằng 60°. Tính thể tích V của khối chóp S.ABC.
A. a 3 3 8
B. a 3 3 24
C. a 3 3 6
D. a 3 3 3
Cho hình chóp S.ABC có SA vuông góc với (ABC) tam giác ABC là tam giác vuông cân tại A,AB 2a góc giữa (SBC) và mặt đáy bằng
60
°
Thể tích khối chóp S.ABC là: A.
125
2
a
3
6
B.
3
6
a
3
4...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với (ABC) tam giác ABC là tam giác vuông cân tại A,AB = 2a góc giữa (SBC) và mặt đáy bằng 60 ° Thể tích khối chóp S.ABC là:
A. 125 2 a 3 6
B. 3 6 a 3 4
C. 16 2 a 3 3
D. 2 6 a 3 3
Cho hình chóp S.ABC có tam giác ABC vuông cân tại
B
,
A
C
a
2
,
mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên
S
A
B
,
S
B
C
tạo với mặt đáy các góc bằng nhau và bằng
60
°
.
Tính theo a thể tích V của...
Đọc tiếp
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B , A C = a 2 , mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên S A B , S B C tạo với mặt đáy các góc bằng nhau và bằng 60 ° . Tính theo a thể tích V của khối chóp S.ABC
A. V = 3 a 3 2
B. V = 3 a 3 4 V = 3 a 3 12
C. V = 3 a 3 6
D. V = 3 a 3 12
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC 2a, góc ACB
60
°
. Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là: A.
a
3
2
B.
a
3
4
C.
a...
Đọc tiếp
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a, góc ACB = 60 ° . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:
A. a 3 2
B. a 3 4
C. a 3 8
D. a 3 16
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh BC2
3
a. Tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là
a
3
, tính góc giữa SA và mặt phẳng (SBC). A.
π
/6 B.
π
/3 C.
π
/4 D. arctan
3
2
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh BC=2 3 a. Tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là a 3 , tính góc giữa SA và mặt phẳng (SBC).
A. π /6
B. π /3
C. π /4
D. arctan 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A,ABACa
3
và góc
A
B
C
⏞
30
°
.Biết SA vuông góc với mặt phẳng đáy và SC2a . Thể tích hình chóp S.ABC là: A.
3
a
3
3
4
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A,AB=AC=a 3 và góc A B C ⏞ = 30 ° .Biết SA vuông góc với mặt phẳng đáy và SC=2a . Thể tích hình chóp S.ABC là:
A. 3 a 3 3 4
B. a 3 3 4
C. a 3 3 2
D. 3 a 3 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC a. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC). Tính sin
α
để thể tích khối chóp S.ABC lớn nhất A.
sin
α
1
3
B.
sin
α
1
3
C.
sin
α
2
3
D.
s...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC = a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Tính sin α để thể tích khối chóp S.ABC lớn nhất
A. sin α = 1 3
B. sin α = 1 3
C. sin α = 2 3
D. sin α = 6 3