Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, S A ⊥ A B C D . Tìm khẳng định sai?
A. A D ⊥ S C
B. S C ⊥ B D
C. S A ⊥ B D
D. S O ⊥ B D
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?
A. S A ⊥ B D .
B. S C ⊥ B D .
C. A D ⊥ S C .
D. S O ⊥ B D .
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC và SB = SD. Khẳng định nào sau đây sai?
A. S O ⊥ A B C D
B. C D ⊥ S B D
C. A B ⊥ S A C
D. C D ⊥ A C
Đáp án B
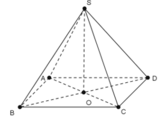
+) Tam giác SAC cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ AC.
+) Tam giác SBD cân tại S có SO là trung tuyến
⇒ SO cũng là đường cao ⇒ SO ⊥ BD.
- Từ đó suy ra SO ⊥ (ABCD).
→ Do ABCD là hình thoi nên CD không vuông góc với BD. Do đó CD không vuông góc với (SBD).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA=SC và SB=SD. Khẳng định nào sau đây sai?
A. C D ⊥ S B D
B. S O ⊥ A B C D
C. B D ⊥ S A
D. A C ⊥ S D
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAC ^ = 60 ° , SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
A. a 3 3 8
B. a 3 3 4
C. a 3 4
D. 3 a 3 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, B A D ^ = 60 0 , S O ⊥ A B C D và mặt phẳng (SCD) tạo với đáy một góc 60 0 . Tính thế tích khối chóp S.ABCD.
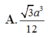
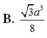
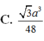
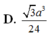
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, ∠ B A D = 60 0 , S O ⊥ ( A B C D ) và mặt phẳng (SCD) tạo với đáy một góc 60 0 . Tính thế tích khối chóp S.ABCD.
A. 3 a 3 12
B. 3 a 3 8
C. 3 a 3 48
D. 3 a 3 24
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB=a, B A D ^ = 60 ° SO ⊥ (ABCD) và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp S.ABCD
A. V S . A B C D = 3 a 3 12
B. V S . A B C D = 3 a 3 24
C. V S . A B C D = 3 a 3 8
D. V S . A B C D = 3 a 3 48
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAD = 60 ° với AC cắt BD tại O, SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
Lời giải:
$\widehat{BAD}=60^0\Rightarrow \widehat{BAO}=30^0$
$\frac{BO}{AB}=\sin \widehat{BAO}=\sin 30^0=\frac{1}{2}$
$\Rightarrow BO=\frac{AB}{2}=\frac{a}{2}$
$BD=2BO=a$
$\frac{AO}{AB}=\cos \widehat{BAO}=\cos 30^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AO=\frac{\sqrt{3}a}{2}$
$\Rightarrow AC=\sqrt{3}a$
$S_{ABCD}=\frac{BD.AC}{2}=\frac{\sqrt{3}a^2}{2}$
$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3a}{4}.\frac{\sqrt{3}a^2}{2}=\frac{\sqrt{3}a^3}{8}$