Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x – 2)2
A. 5 2
B. 2
C. 2 5
D. 4
Cho hàm số:
y = x 3 + 3 2 x 2
Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:
A. d = 2 5 B. d = 5 /4
C. d = 5 D. 5 /2
Đáp án: D.
y' = 3 x 2 + 3x = 3x(x + 1) = 0
⇔ 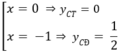
Vậy khoảng cách giữa hai điểm cực trị là:
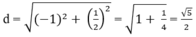
Cho hàm số y=x4-2( m2-m+1)x2+m-1 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu ngắn nhất.
A. m= -1/2
B. m= 1/2
C. m=2
D. m=1
Ta có
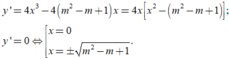
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó 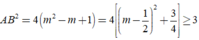
Dấu xảy ra khi m=1/2.
Chọn B.
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Cho hàm số:
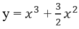
Khoảng cách d giữa hai điểm cực trị của đồ thị hàm số là:
A. d = 2 5 B. d = 5 /4
C. d = 5 D. 5 /2
Đáp án: D.
y' = 3 x 2 + 3x = 3x(x + 1) = 0
⇔ 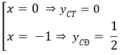
Vậy khoảng cách giữa hai điểm cực trị là:
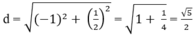
Tính theo m khoảng cách giữa điểm cực đại và điểm cực tiểu ( nếu có) của đồ thị hàm số: y = 1 3 x 3 - m x 2 - x + m + 1
A. 2 3 ( m 2 + 1 ) ( 4 m 4 + 5 m 2 + 9 )
B. 4 9 ( 2 m 2 + 1 ) ( 4 m 4 + 8 m 2 + 13 )
C. 2 3 ( m 2 + 1 ) ( 4 m 4 + 8 m 2 + 13 )
D. ( 4 m 2 + 4 ) ( 4 m 4 + 8 m 2 + 10 )
Tìm các giá trị của tham số m để hàm số y = 2 x 4 - 16 m x 2 - 1 có hai cực tiểu và khoảng cách giữa 2 điểm cực tiểu của đồ thị bằng 10
A. m = - 25 4
B. m = 625
C. m = 25 4
D. m = - 625
Cho hàm số y = x 4 − 2 x 2 − 4 có đồ thị (C). Gọi h 1 là khoảng cách giữa hai điểm cực tiểu của (C) và h 2 là khoảng cách từ điểm cực đại của (C) tới trục hoành. Tỉ số h 1 h 2 là
A. 1 2 .
B. 5 4 .
C. 5 2 .
D. 4 5 .