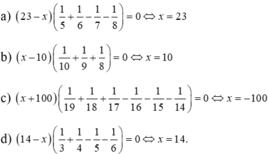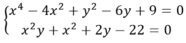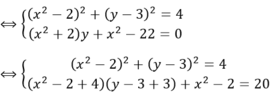6+x4=22

Những câu hỏi liên quan
Bài 2: Phân tích đa thức thành nhân tử:1) 6x3y - 12x2y2 + 6xy3 6) x – x -22) (x2 +4)2 -16 7) x4 - 5x2 + 43) 5x2 - 5xy - 10x + 10y 8) x2 – x3 - 2x2 - x4) a3 - 3a + 3b – b3 9) (a3 – 27) – (3 – a)(6a + 9)5) x2 - 2x – y2 +1 10) x2(y – z) + y2(z – x) + z2(x – y)
Đọc tiếp
Bài 2: Phân tích đa thức thành nhân tử:
1) 6x3y - 12x2y2 + 6xy3 6) x – x -2
2) (x2 +4)2 -16 7) x4 - 5x2 + 4
3) 5x2 - 5xy - 10x + 10y 8) x2 – x3 - 2x2 - x
4) a3 - 3a + 3b – b3 9) (a3 – 27) – (3 – a)(6a + 9)
5) x2 - 2x – y2 +1 10) x2(y – z) + y2(z – x) + z2(x – y)
\(1,=6xy\left(x^2-2xy+y^2\right)=6xy\left(x-y\right)^2\\ 2,=\left(x^2+4-4\right)\left(x^2+4+4\right)=x^2\left(x^2+8\right)\\ 3,=5x\left(x-y\right)-10\left(x-y\right)=5\left(x-2\right)\left(x-y\right)\\ 4,=\left(a-b\right)\left(a^2+ab+b^2\right)-3\left(a-b\right)=\left(a-b\right)\left(a^2+ab+b^2-3\right)\\ 5,=\left(x-1\right)^2-y^2=\left(x+y-1\right)\left(x-y-1\right)\\ 6,Sửa:x^2-x-2=x^2+x-2x-2=\left(x+1\right)\left(x-2\right)\\ 7,=x^4-4x^2-x^2+4=\left(x^2-4\right)\left(x^2-1\right)\\ =\left(x-2\right)\left(x+2\right)\left(x-1\right)\left(x+1\right)\\ 8,=-x^3-x^2-x=-x\left(x^2+x+1\right)\\ 9,=\left(a-3\right)\left(a^2+3a+9\right)+\left(a-3\right)\left(6a+9\right)\\ =\left(a-3\right)\left(a^2+9a+18\right)\\ =\left(a-3\right)\left(a^2+3a+6a+18\right)\\ =\left(a-3\right)\left(a+3\right)\left(a+6\right)\)
\(10,=x^2y-x^2z+y^2z-xy^2+z^2\left(x-y\right)\\ =xy\left(x-y\right)-z\left(x-y\right)\left(x+y\right)+z^2\left(x-y\right)\\ =\left(x-y\right)\left(xy-xz-yz+z^2\right)\\ =\left(x-y\right)\left(x-z\right)\left(y-z\right)\)
Đúng 0
Bình luận (0)
Phương trình
−
x
4
−
2
2
−
1
x
2
+
3
−
2
2
0
có bao nhiêu nghiệm? A. 2 B. 3 C. 4 D. 0
Đọc tiếp
Phương trình − x 4 − 2 2 − 1 x 2 + 3 − 2 2 = 0 có bao nhiêu nghiệm?
A. 2
B. 3
C. 4
D. 0
Đặt t = x 2 t ≥ 0
Phương trình (1) thành − t 2 − 2 ( 2 − 1 ) t + ( 3 − 2 2 ) = 0 ( 2 )
Phương trình (2) có a . c = ( − 1 ) ( 3 − 2 2 ) < 0
Suy ra phương trình (2) có 2 nghiệm trái dấu
Suy ra phương trình ban đầu có 2 nghiệm phân biệt.
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Phương trình
−
x
4
−
2
2
−
1
x
2
+
3
−
2
2
0
có tổng các nghiệm bằng? A. 2 B.
−
2
2
−
1...
Đọc tiếp
Phương trình − x 4 − 2 2 − 1 x 2 + 3 − 2 2 = 0 có tổng các nghiệm bằng?
A. 2
B. − 2 2 − 1
C. 2 − 1
D. 0
Đặt t = x 2 t ≥ 0
Phương trình (1) thành − t 2 − 2 ( 2 − 1 ) t + ( 3 − 2 2 ) = 0 ( 2 )
Phương trình (2) có a . c = ( − 1 ) ( 3 − 2 2 ) < 0
Suy ra phương trình (2) có 2 nghiệm trái dấu t 1 < 0 < t 2
Suy ra phương trình đầu có 2 nghiệm phân biệt x 1 , 2 = ± t 2 ⇒ x 1 + x 2 = 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
tính bằng cách thuận tiện nhất
a) 4 giờ 22 phút x 4 + 5 giờ 38 phút x4
b) 7 phút 30 giây x 7 - 6 phút 30 giây x 7
a) 4 giờ 22 phút x 4 + 5 giờ 38 phút x 4
= ( 4 giờ 22 phút + 5 giờ 38 phút ) x 4
= 10 giờ x 4
=40 giờ
b) 7 phút 30 giây x 7 - 6 phút 30 giây x 7
= ( 7 phút 30 giây - 6 phút 30 giây ) x 7
= 1 phút x 7
= 7 phút
Kết bn với mik nha!
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
18
−
x
5
+
17
−
x
6
16
−
x
7
+
15
−
x
8
;
b)
x
−...
Đọc tiếp
Giải các phương trình sau:
a) 18 − x 5 + 17 − x 6 = 16 − x 7 + 15 − x 8 ;
b) x − 30 10 + x − 28 9 + x − 26 8 = − 6 ;
c) x + 81 19 + x + 82 18 + x + 83 17 = x + 84 16 + x + 85 15 + x + 86 14 ;
d) 20 − x 3 + 22 − x 4 = 24 − x 5 + 26 − x 6 .
Số nghiệm của hệ phương trình
x
4
-
4
x
2
+
y
2
-
6
y
+
9...
Đọc tiếp
Số nghiệm của hệ phương trình x 4 - 4 x 2 + y 2 - 6 y + 9 = 0 x 2 y + x 2 + 2 y - 22 = 0 là:
A. 4
B. 1
C. 2
D. 3
Rút gọn:
1) x2 - 2x + 1 / x3 -1 + x2 - 1 / ( x - 1 )2
2) x4 - 2x2y2 + y4 / x3 - y3
1: \(=\dfrac{x-1}{x^2+x+1}+\dfrac{x+1}{x-1}\)
\(=\dfrac{x^2-2x+1+x^3+x^2+x^2+x+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3+3x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
2: \(=\dfrac{\left(x^2-y^2\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{\left(x-y\right)\left(x+y\right)^2}{x^2+xy+y^2}\)
Đúng 1
Bình luận (0)
Cộng các phép tính:
(h: giờ ; p:phút)
40p 100 giây : 6 =
56p 72 giây - 10p 2 giây =
10p 22 giây + 3p 58 giây =
11p 16 giây x 3 =
3 năm 4 tháng x 3 =
12 ngày 3 giờ x 3 =
12 ngày 8 giờ x4 =
Cộng các phép tính:
(h: giờ ; p:phút)
40p 100 giây : 6 =
56p 72 giây - 10p 2 giây =
10p 22 giây + 3p 58 giây =
11p 16 giây x 3 =
3 năm 4 tháng x 3 =
12 ngày 3 giờ x 3 =
12 ngày 8 giờ x4 =