Hãy chọn câu đúng. Hai ΔABC và ΔDEF có A ^ = 80 ∘ , B ^ = 70 ∘ , F ^ = 30 ∘ ; BC = 6cm. Nếu ΔABC đồng dạng với ΔDEF thì:
A. D ^ = 170 ∘ ; EF = 6cm
B. E ^ = 80 ∘ ; ED = 6cm
C. D ^ = 70 ∘
D. C ^ = 30 ∘
Những câu hỏi liên quan
Hãy chọn câu đúng. Nếu ΔABC và ΔDEF có góc B D;
B
A
B
C
D
E
D
F
thì: A. ΔABC đồng dạng với ΔDEF B. ΔABC đồng dạng với ΔEDF C. ΔBCA đồng dạng với ΔDEF D. ΔABC đồng dạng với ΔFDE
Đọc tiếp
Hãy chọn câu đúng. Nếu ΔABC và ΔDEF có góc B = D; B A B C = D E D F thì:
A. ΔABC đồng dạng với ΔDEF
B. ΔABC đồng dạng với ΔEDF
C. ΔBCA đồng dạng với ΔDEF
D. ΔABC đồng dạng với ΔFDE
ΔABC và ΔDEF có góc B = D; B A B C = D E D F thì ΔABC đồng dạng với ΔEDF
Đáp án: B
Đúng 0
Bình luận (0)
Cho ΔABC và ΔDEF có góc B = D; B A B C = D E D F , chọn kết luận đúng:
A. ΔABC ~ ΔDEF
B. ΔABC ~ ΔEDF
C. ΔBAC ~ ΔDFE
D. ΔABC ~ ΔFDE
ΔABC và ΔDEF có góc B = D; B A B C = D E D F thì ΔABC đồng dạng với ΔEDF
Đáp án: B
Đúng 0
Bình luận (0)
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...b) Nếu
Δ
A
B
C
~
Δ
D
E
F
với tỉ số đồng dạng là 1/2 và
Δ
D
E
F
~
Δ
M
N
P
với tỉ số đồng dạng là 4/3 thì
Δ
M
N
P...
Đọc tiếp
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu Δ A B C ~ Δ D E F với tỉ số đồng dạng là 1/2 và Δ D E F ~ Δ M N P với tỉ số đồng dạng là 4/3 thì Δ M N P ~ Δ A B C với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho A I / A B = A K / B C t h ì I K / / B C . . . .
d) Hai tam giác đồng dạng thì bằng nhau....
24 tháng 10 2021 lúc 19:37
ΔABC và ΔDEF có AB ED, BC EF. Thêm điều kiện nào sau đây để ΔABCΔDEF ? · A. · B. · C. AB AC· D. AC DFGIÚP LINH VỚI ;-;
Đọc tiếp
ΔABC và ΔDEF có AB = ED, BC = EF. Thêm điều kiện nào sau đây để ΔABC=ΔDEF ?
· A. 
=
· B. 
=
· C. AB = AC
· D. AC = DF
GIÚP LINH VỚI ;-;
Cho ΔABC đồng dạng với ΔDEF và
A
^
80
∘
,
C
^
70
∘
, AC 6cm. Số đo góc
E
^
là: A.
80
∘
B.
30
∘
C.
70
∘
D.
50...
Đọc tiếp
Cho ΔABC đồng dạng với ΔDEF và A ^ = 80 ∘ , C ^ = 70 ∘ , AC = 6cm. Số đo góc E ^ là:
A. 80 ∘
B. 30 ∘
C. 70 ∘
D. 50 ∘
Xét tam giác ABC có: A ^ + B ^ + C ^ = 180 ∘
⇒ B ^ = 180 ∘ – A ^ + C ^ = 180 ∘ – ( 80 ∘ + 70 ∘ ) = 30 ∘
Mà tam giác ABC đồng dạng với tam giác DEF nên E ^ = B ^ = 30 ∘
Vậy E ^ = 30 ∘
Đáp án: B
Đúng 0
Bình luận (0)
cho ΔABC và ΔDEF có AB=EF và BC=DE
A) Muốn ΔABC và ΔDEF bằng nhau theo trường hợp c_g_c thì cần thiếu điều kiện nào( đủ 1 điều kiện)
B) giả sữ ΔABC có góc c= 54 độ; AC= 6cm. Tính số đo của cạnh góc tương ứng trong ΔDEF
a: \(\widehat{B}=\widehat{E}\)
Đúng 0
Bình luận (0)
Câu 30: Cho ΔABC = ΔDEF, biết 0 A 50 = , 0 B 65 = . Hỏi ΔDEF là tam giác gì ?
ta có góc C có số đo là :
\(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-50^0-65^0=65^0\)
Do góc C bằng góc B nên tam giác ABC cân tại A
Do đó tam giác tương ứng là DEF cân tại đỉnh D
Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4:5:6 . Cho biết
Δ
D
EF
∽
Δ
A
B
C
và cạnh nhỏ nhất của
Δ
D
E
F
l
à
0
,
8
m
, hãy tính các cạnh còn lại của
Δ
D
E
F
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4:5:6 . Cho biết Δ D EF ∽ Δ A B C và cạnh nhỏ nhất của Δ D E F l à 0 , 8 m , hãy tính các cạnh còn lại của Δ D E F
Vì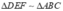 
nên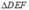 
cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
Giả sử DE < EF < FD Þ DE = 0,8m.
Ta có
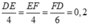
Từ đó tính được EF = 1m và FD = 1,2m
Đúng 0
Bình luận (0)
ΔABC và ΔDEF có \(\dfrac{AB}{ED}=\dfrac{AC}{EF}\) ; A=E vậy ΔABC∼....
