Trên trục x'Ox cho 4 điểm A(-2) ; B(4); C(1); D(6)

Những câu hỏi liên quan
Trên trục x'Ox cho 4 điểm M,A,B,C : CHỨNG MINH
\(\overrightarrow{MA}^2.\overrightarrow{BC}+\overrightarrow{MB}^2.\overrightarrow{CA}+\overrightarrow{MC}^2.\overrightarrow{AB}+\overrightarrow{AB}.\overrightarrow{BC}.\overrightarrow{CA}=\overrightarrow{0}\)
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
-
1
;
2
;
-
1
. Hình chiếu vuông góc của A trên trục toạ độ
x
O
x
là A.
M
0
;
2
;
-
1
B.
M...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A - 1 ; 2 ; - 1 . Hình chiếu vuông góc của A trên trục toạ độ x ' O x là
A. M 0 ; 2 ; - 1
B. M - 1 ; 0 ; 0
C. P 0 ; 2 ; 0
D. Q 0 ; 0 ; - 1
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
-
1
;
2
;
-
1
. Hình chiếu vuông góc của A trên trục toạ độ
x
O
x
là A.
M
0
;
2
;
-
1
B.
M...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A - 1 ; 2 ; - 1 . Hình chiếu vuông góc của A trên trục toạ độ x ' O x là
A. M 0 ; 2 ; - 1
B. M - 1 ; 0 ; 0
C. P 0 ; 2 ; 0
D. Q 0 ; 0 ; - 1
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
-
1
;
2
;
-
1
. Hình chiếu vuông góc của A trên trục toạ độ
x
O
x
là A.
M
0
;
2
;
-
1
B.
M...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A - 1 ; 2 ; - 1 . Hình chiếu vuông góc của A trên trục toạ độ x ' O x là
A. M 0 ; 2 ; - 1
B. M - 1 ; 0 ; 0
C. P 0 ; 2 ; 0
D. Q 0 ; 0 ; - 1
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-1;2;-1). Hình chiếu vuông góc của A trên trục toạ độ x'Ox là
A. M(0;2;-1).
B. N(-1;0;0).
C. P(0;2;0).
D. Q(0;0;-1).
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
-
1
;
2
;
-
1
. Hình chiếu vuông góc của A trên trục toạ độ
x
O
x
là A.
30
°
B.
120
°
C.
60
°
D. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A - 1 ; 2 ; - 1 . Hình chiếu vuông góc của A trên trục toạ độ x ' O x là
A. 30 °
B. 120 °
C. 60 °
D. 150 °
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
-
1
;
2
;
-
1
. Hình chiếu vuông góc của A trên trục toạ độ
x
O
x
là A.
30
°
B.
120
°
C.
60
°
D. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A - 1 ; 2 ; - 1 . Hình chiếu vuông góc của A trên trục toạ độ x ' O x là
A. 30 °
B. 120 °
C. 60 °
D. 150 °
Trong không gian Oxyz cho điểm M (1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục xOx, yOy, zOz lần lượt tại ba điểm phân biệt A, B, C sao cho OA OB OC ≠ 0. A. 1. B. 2. C. 4 D. 3.
Đọc tiếp
Trong không gian Oxyz cho điểm M (1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x'Ox, y'Oy, z'Oz lần lượt tại ba điểm phân biệt A, B, C sao cho OA = OB = OC ≠ 0.
A. 1.
B. 2.
C. 4
D. 3.
Chọn D
Gọi A (a;0;0), B (0;b;0); C (0;0;c). Ta có OA = |a|; |OB| = b; |OC| = |c|.
Phương trình mặt phẳng đi qua ba điểm A, B, C là ![]()
Theo giả thiết ta có điểm 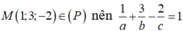
Vì OA=OB=OC => |a| = |b| = |c| nên ta có hệ phương trình
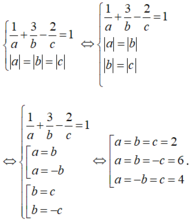
Vậy có 3 mặt phẳng thỏa mãn.
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho điểm M (3; 2; 1). Viết phương trình mặt phẳng đi qua M và cắt các trục xOx, yOy, zOz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC. A. 3x + y + 2z - 14 0 B. 3x + 2y + z - 14 0
C
.
x
9
+
y
3
+
z
6
1
D
.
x
12...
Đọc tiếp
Trong không gian Oxyz cho điểm M (3; 2; 1). Viết phương trình mặt phẳng đi qua M và cắt các trục x'Ox, y'Oy, z'Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC.
A. 3x + y + 2z - 14 = 0
B. 3x + 2y + z - 14 = 0
C . x 9 + y 3 + z 6 = 1
D . x 12 + y 4 + z 4 = 1
Chọn B
Giả sử A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c ≠ 0
Phương trình mặt phẳng (P) qua A, B, C có dạng: ![]()
Vì (P) đi qua M (3; 2; 1) nên ta có: 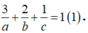

Vậy phương trình mặt phẳng (P):
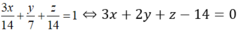
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho điểm M(1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục xOx, yOy,zOz lần lượt tại ba điểm phân biệt A, B, C sao cho OAOBOC
≠
0 A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Trong không gian Oxyz cho điểm M(1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x'Ox, y'Oy,z'Oz lần lượt tại ba điểm phân biệt A, B, C sao cho OA=OB=OC ≠ 0
A. 3
B. 2
C. 1
D. 4
Đáp án D
Phương pháp
Gọi A(a;0;0), B(0;b;0), C(0;0;c)
![]()
Chia các trường hợp để phá trị tuyệt đối và viết phương trình mặt phẳng (P) dạng đoạn chắn.
Cách giải: Giả sử A(a;0;0), B(0;b;0), C(0;0;c)
![]()
![]()
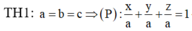
![]()
![]()
![]()
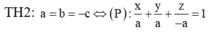
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
Vậy có 4 mặt phẳng thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)