Tìm tập nghiệm S của phương trình x - 1 x - 2 x x + 1 = 0
A. S = {1;2;–1}
B. S = {1;–1}
C. S = {1;2}
D. S = {2;–1}
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Gọi S là tập nghiệm của phương trình log 5 ( x + 1 ) + log 5 ( x - 3 ) = 1 Tìm S
A. S = - 2 ; 4
B. S = - 1 + 13 2 ; - 1 - 13 2
C. S = 4
D. S = - 1 + 13 2
Gọi S là tập nghiệm của phương trình log5(x+1) + log5( x-3) = 1. Tìm S
A.S= {-2; 4}
B. 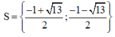
C. S= {4}
D. 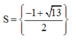
Chọn C
Điều kiện
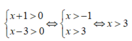
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .
Tìm tập nghiệm S của phương trình l o g 2 ( x - 1 ) + l o g 2 ( x + 1 ) = 3
A . S = - 3 ; 3
B . S = 10
C . S = 3
D . S = - 10 ; 10
Tìm tập nghiệm S của phương trình log 6 x 5 - x = 1
A. S={2;3}.
B. S={2;3;-1}.
C. S={2;-6}.
D. S={2;3;4}.
Tìm tập nghiệm S của phương trình log 6 x 5 − x = 1
A. S = 2 ; − 6
B. S = 2 ; 3 ; 4
C. S = 2 ; 3
D. S = 2 ; 3 ; − 1
Đáp án C
Phương pháp: Cách giải phương trình log a f x = b ⇔ f x = a b 0 < a ≠ 1 ; f x > 0
Cách giải: Điều kiện: x 5 − x > 0 ⇔ 0 < x < 5
log 6 x 5 − x = 1 ⇔ x 5 − x = 6 ⇔ x 2 − 5 x + 6 = 0 ⇔ x = 2 x = 3 t m
Vậy S = 2 ; 3
Tìm tập nghiệm S của phương trình log 6 x 5 - x = 1
![]()
![]()
![]()
![]()
Tìm tập nghiệm S của phương trình log 1 2 ( x + 2 ) - log 1 2 ( x ) > log 2 x 2 - x - 1
D. (1; 2]
A. 2 ; + ∞
B. (1;2)
C. (0;2)
D. (1; 2]
Tìm tập nghiệm S của bất phương trình log0,2 (x – 1) < log0,2 (3 – x).
A. S = - ∞ ; 3
B. S = 2 ; 3
C. S = 2 ; + ∞
D. S = 1 ; 2
Tìm tập nghiệm S của phương trình log 2 ( x - 1 ) = log 2 ( 2 x + 1 ) .
A. S = 2
B. S = ∅
C. S = {-2}
D. S = {0}