Chọn C
Điều kiện
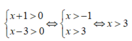
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .
Chọn C
Điều kiện
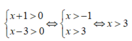
Ta có: log5(x+1) + log5( x-3) = 1
Tương đương : log5[(x+1)( x-3)] = 1 hay ( x+1) (x-3) = 5
=> x2- 3x+ x- 3= 5 nên x2- 2x-8= 0
Do đó; x= -2 hoặc x= 4
Mà x= -2 loại do đó đáp án đúng là C .
Giải bất phương trình log 5 - 1 4 x - 3 > log 5 - 1 2 x - 1 Chọn tập nghiệm S của bất phương trình.
A. 3 4 , 1
B. 1 , + ∞
C. 1 2 , 1
D. 3 4 , + ∞
Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log5( x2 + 1) > log5( x2 + 4x + m) - 1 (1)
A. -12 ≤ m ≤ 13
B. 12 < m < 13
C. -12 < m < 12
D. Đáp án khác
Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log 5 ( x 2 + 1 ) ≥ log 5 ( m x 2 + 4 x + m ) có nghiệm đúng ∀ x
A. m ∈ ( 2 ; 3 ]
B. m ∈ ( - 2 ; 3 ]
C. m ∈ [ 2 ; 3 )
D. m ∈ [ - 2 ; 3 )
Cho phương trình log 5 ( x + 4 ) = 3 . Nghiệm của phương trình này nằm trong khoảng nào sau đây?
A. (100; 125)
B. (10; 20)
C. (200; 250)
D. (125; 150)
Giải bất phương trình log 5 ( 2 x - 4 ) < log 5 ( x + 3 )
A. 2 < x < 7
B. -3 < x < 7
C. -3 < x < 2
D. x < 7
Gọi S là tập nghiệm của phương trình 2 ( 2 x - 1 ) - 5 . 2 ( x - 1 ) + 3 = 0 . Tìm S.
A. S = {1; log23 }
B. S = {0; log 2 3 }
C. S = {1; log 3 2 }
D. S = {1}
Phương trình log 5 x + 5 = 2 có nghiệm là
A. x = 20
B. x = 5
C. x = 27
D. x = 30
Giải phương trình log 5 ( x + 4 ) = 3
A. x = 11
B. x = 121
C. x = 239
D. x = 129
Cho phương trình 5 x + m = log 5 x - m với m là tham số. Có bao nhiêu giá trị nguyên của m ∈ - 20 ; 20 để phương trình đã cho có nghiệm?
A. 20.
B. 19.
C. 9.
D. 21.