
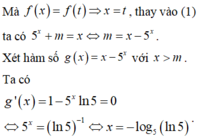
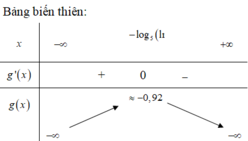
Dựa vào bảng biến thiên ta có phương trình đã cho có nghiệm khi m ≤ - 0 , 92 .
Mặt khác m nguyên và m ∈ - 20 ; 20 vì vậy m = - 19 ; - 18 ; . . . ; - 1 nên có 19 giá trị m cần tìm.
Đáp án B.

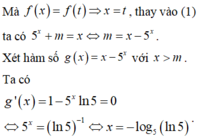

Dựa vào bảng biến thiên ta có phương trình đã cho có nghiệm khi m ≤ - 0 , 92 .
Mặt khác m nguyên và m ∈ - 20 ; 20 vì vậy m = - 19 ; - 18 ; . . . ; - 1 nên có 19 giá trị m cần tìm.
Đáp án B.
Cho phương trình 5x+m = log5(x-m) với m là tham số. Có bao nhiêu giá trị nguyên của m ∈ ( - 20 ; 20 ) để phương trình đã cho có nghiệm?
A. 19.
B. 9.
C. 21.
D. 20.
Cho phương trình
5
x
+
m
=
log
5
x
-
m
với m là tham số. Có bao nhiêu giá trị nguyên của ![]() để phương trình đã cho có nghiệm?
để phương trình đã cho có nghiệm?
A. 20
B. 19
C. 9
D. 21
Có bao nhiêu giá trị nguyên dương của m < 20 để bất phương trình log 2 x 2 + 2 3 x 2 + 4 x + m ≤ x 2 + 4 x + m - 5 có nghiệm ∀ x ∈ R .
A. 15.
B.12
C.14
D.13
Có bao nhiêu giá trị nguyên dương của m < 20 để bất phương trình log 2 x 2 + 2 3 x 2 + 4 x + m ≤ x 2 + 4 x + m - 5 có nghiệm ∀ x ∈ ℝ .
A. 15
B. 12
C. 14
D. 13
Có bao nhiêu giá trị nguyên của tham số m để phương trình log 2 ( x 2 - 2 x + 5 ) - m . log x 2 - 2 x + 5 2 = 5 có hai nghiệm phân biệt là nghiệm của bất phương trình log 2017 ( x + 1 ) - log 2017 ( x - 1 ) > log 2017 4
A. 0
B. 1
C. 3
D. 2
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d với a, b, c, d là các số thực, có đồ thị như hình bên.
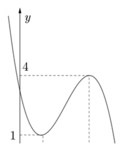
Có bao nhiêu giá trị nguyên của tham số m để phương trình f e x 2 = m có ba nghiệm phân biệt?
A. Vô số.
B. 3.
C. 1.
D. 2.
Cho phương trình 4 x - 2 x + 2 + m - 2 = 0 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt x 1 , x 2 thỏa mãn 0 ≤ x 1 < x 2
A.1
B.3
C.2
D.0
Cho phương trình m + 2 2 + x - 2 2 - x + 3 x + 4 4 - x 2 = m + 12 . Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm thực phân biệt là
A. 3
B. 4
C. 2.
D. 5
Cho phương trình m . 2 x 2 - 5 x + 6 + 2 1 - x 2 = 2 . 2 6 - 5 x + m với m là tham số thực. Có tất cả bao nhiêu giá trị của m để phương trình có đúng ba nghiệm phân biệt.
A. 1.
B. 2.
C. 3.
D. 4.