Giả sử . Tính A. 1 B. n C. (n+1)! D. n!
Đọc tiếp
Giả sử 
. Tính 
A. 1
B. n
C. (n+1)!
D. n!
Những câu hỏi liên quan
a^bb^cc^dd^ee^a
giả sử a bLeftrightarrow bcLeftrightarrow c dLeftrightarrow deLeftrightarrow e aLeftrightarrow ab ( trái với giả sử , loại )
giả sử abLeftrightarrow b cLeftrightarrow cdLeftrightarrow d eLeftrightarrow eaLeftrightarrow a b ( lại trái với giả sử , loại )
nên a b
+ nếu a b 1 Rightarrow1^11^cc^dd^ee^1
Rightarrow edc1
Rightarrow abcde1
+ nếu a b ge2 . có a^bb^c mà a b ge2 Rightarrow bc
lại có b^cc^d mà b c nên c d
lại có c^dd^e mà c d nên d e
Rightarrow abcde
vậy...
Đọc tiếp
\(a^b=b^c=c^d=d^e=e^a\)
giả sử \(a< b\Leftrightarrow b>c\Leftrightarrow c< d\Leftrightarrow d>e\Leftrightarrow e< a\Leftrightarrow a>b\) ( trái với giả sử , loại )
giả sử \(a>b\Leftrightarrow b< c\Leftrightarrow c>d\Leftrightarrow d< e\Leftrightarrow e>a\Leftrightarrow a< b\) ( lại trái với giả sử , loại )
nên a = b
+ nếu a = b = 1 \(\Rightarrow1^1=1^c=c^d=d^e=e^1\)
\(\Rightarrow e=d=c=1\)
\(\Rightarrow a=b=c=d=e=1\)
+ nếu a = b \(\ge2\) . có \(a^b=b^c\) mà a = b \(\ge2\) \(\Rightarrow b=c\)
lại có \(b^c=c^d\) mà b = c nên c = d
lại có \(c^d=d^e\) mà c = d nên d = e
\(\Rightarrow a=b=c=d=e\)
vậy a = b = c = d = e với \(a^b=b^c=c^d=d^e=e^a\)
Giả sử
∫
1
2
1
+
x
2
x
4
d
x
1
c
a
a
-
b
b
+
c...
Đọc tiếp
Giả sử ∫ 1 2 1 + x 2 x 4 d x = 1 c a a - b b + c b a ; b ; c ∈ N ; 1 ≤ a , b , c ≤ 9 . Tính giá trị biểu thức S = C 2 a + c b - a
A. 165
B. 715
C. 5456
D. 35
Câu 1:
a, Giả sử n là số tự nhiên thỏa mãn điều kiện n(n+1) +6 không chia hết cho 3. Chứng minh rằng 2n^2+n+8 không là số chính phương
b, cho 4 số dương a;b;c;d thỏa mãn điều kiện a^4/b + c^4/d = 1/(b+d) và a^2 + c^2 =1 . Chứng minh rằng (a^2014)/(b^1007) + ( c^ 2014)/(d^1007) = 2/( b+d)^1007
.Mọi người giải giúp Linh nha ^^ Linh đang cần gấp ạ!
Giả sử N,a,b,c là các sô nguyên thoả mãn 1<a<b<c<N . Có bao nhiêu so nguyên trong đoạn từ 1 đến N chia hết cho ít nhất một trong ba số a,b,c
1. Dòng nào nói đúng những nghệ thuật đặc sắc trong phần tác giả khẳng định lợi thế của thành Đại La ? ( chọn nhiều đáp án)
A. Sử dụng thể văn biền ngẫu và phép liệt kê
B. Sử dụng những từ ngữ mang tính chất ngợi ca.
C. Sử dụng phép nói quá
D. Đan xen câu dài với câu ngắn
Xem chi tiết
Cho hình chữ nhật $A B C D$ biết $A D=1$. Giả sử $\mathrm{E}$ là trung điểm $\mathrm{AB}$ và thỏa mãn $\sin \widehat{B D E}=\dfrac{1}{3}$.
Tính độ dài cạnh $A B$.
1. Cho góc xAy90 độ.Trên Ax lấy 2 điểm B và C(ABAC). Trên Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AB4, BC2,5, DE13,5. Tính AE.
2. Cho góc xAy90 độ.Trên Ax lấy 2 điểm B và C(ABAC). Trên Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AB5, AC7,5, DE2. Tính AD.
3. Cho góc xAy90 độ.Trên Ax lấy 2 điểm B và C(ABAC). Trên Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AC18, BC12, AD3.Tính AE.
Đọc tiếp
1. Cho góc xAy<90 độ.Trên Ax lấy 2 điểm B và C(AB<AC). Trên Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AB=4, BC=2,5, DE=13,5. Tính AE.
2. Cho góc xAy<90 độ.Trên Ax lấy 2 điểm B và C(AB<AC). Trên Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AB=5, AC=7,5, DE=2. Tính AD.
3. Cho góc xAy<90 độ.Trên Ax lấy 2 điểm B và C(AB<AC). Trên Ay lấy 2 điểm D và E sao cho BD//CE. Giả sử AC=18, BC=12, AD=3.Tính AE.
giả sử a,b,c,d là 4 số nguyên bất kì.Chứng minh rằng (b-a)(c-a)(d-a)(d-b)(d-c)(c-b)chia hết cho 12
bài này chép mạng vô nghĩa nhé !
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: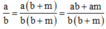 
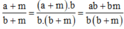
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó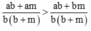 
Hay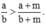 
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
