Cho hình chóp S.ABC có SA = SB = SC = a 3 2 đáy là tam giác vuông tại A, cạnh BC = a. Tính côsin của góc giữa đường thẳng SA và mặt phẳng (ABC)
A. 1 3
B. 1 3
C. 3 2
D. 1 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB = a 10 , BC = 2a, SC = 2a 3 . Thể tích khối chóp S.ABC là:
A . 3 a 3 2
B . 3 a 3 2
C . 3 a 3
D . a 3
Cho hình chóp S.ABC có SA=SB=SC= a 3 2 , đáy là tam giác vuông tại A, cạnh BC=a. Tính côsin của góc giữa đường thẳng SA và mặt phẳng (ABC).
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB= a 10 ;BC=2a;SC=2a 3 Thể tích khối chóp S.ABC là:
A. 3 a 3 2
B. 3 a 3 2
C. 3 a 3
D. a 3
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.

A. k = 1 3
B. k = 2 4
C. k = 4 9
D. k = 2 3
Đáp án C
Do CS = CB nên B’ là trung điểm của SB.
Ta có:
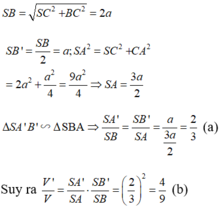
iowhjeb h2ndb ewdnbw2hejwgbdwdwdhewdd
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.
A. V = 14 54 a 3
B. V = 14 64 a 3
C. V = 14 49 a 3
D. V = 4 61 a 3
Đáp án A
Áp dụng ví dụ 2, ta có:

Từ đó suy ra
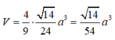
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB=BC=a . Cạnh bên SA vuông góc với mặt phẳng đáy, SA =a căn 2
a) CM BC vuông SB
b) Xác định và tính góc giữa SC và (ABC)
a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN
A. V = a 3 36
B. V = a 3 5 15
C. V = a 3 3 18
D. V = a 3 30
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = a , B C = 2 a .Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN.

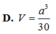
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)