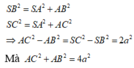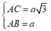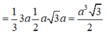= 3a
Các câu hỏi tương tự
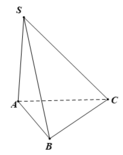
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB AC a
3
và góc
A
B
C
^
30
0
.Biết SA vuông góc với mặt phẳng đáy và SC 2a. Thể tích hình chóp là:
A
.
3
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB = AC = a 3 và góc A B C ^ = 30 0 .Biết SA vuông góc với mặt phẳng đáy và SC = 2a. Thể tích hình chóp là:
A . 3 a 3 3 4
B . a 3 3 4
C . a 3 3 2
D . 3 a 3 3 2
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB a, BC a
3
, biết SA a và vuông góc với mặt phẳng đáy. Một mặt phẳng (
α
) đi qua A , vuông góc với SC tại H , cắt SB tại K . Tính thể tích khối chóp S.AHK theo a
A
.
a
3
3
30
B
.
5...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a, BC = a 3 , biết SA = a và vuông góc với mặt phẳng đáy. Một mặt phẳng ( α ) đi qua A , vuông góc với SC tại H , cắt SB tại K . Tính thể tích khối chóp S.AHK theo a
A . a 3 3 30
B . 5 a 3 3 60
C . a 3 3 60
D . a 3 3 10
Cho hình chóp S.ABC có SC 2a,
S
C
⊥
(
A
B
C
)
Đáy ABC là tam giác vuông cân tại B và có
(
α
)
Mặt phẳng
(
α
)
đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE. A.
4...
Đọc tiếp
Cho hình chóp S.ABC có SC= 2a, S C ⊥ ( A B C ) Đáy ABC là tam giác vuông cân tại B và có ( α ) Mặt phẳng ( α ) đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE.
A. 4 a 3 9
B. 2 a 3 3
C. 2 a 3 9
D. a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết Tính thể tích V của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết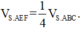 
Tính thể tích V của khối chóp S.ABC
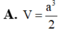
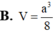
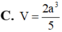
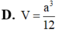
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB a, BC a
3
Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng
5
a
2
3
2
. Tính theo a khoảng cách d từ A đến mặt...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB =a, BC =a 3 Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72a
B. 0,9a
C. 0,8a
D. 1,12a
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, ABa, AC2a, cạnh bên SA vuông góc với mặt đáy và SAa. Tính thể tích V của khối chóp S.ABC .
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=2a, cạnh bên SA vuông góc với mặt đáy và SA=a. Tính thể tích V của khối chóp S.ABC .
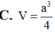
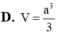
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB 3a, BC 4a, mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB 2a
3
và
S
B
C
^
30
0
. Tính khoảng cách từ B đến mặt phẳng (SAC) theo a.
A
.
...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a, mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB = 2a 3 và S B C ^ = 30 0 . Tính khoảng cách từ B đến mặt phẳng (SAC) theo a.
A . 3 a 5
B . a 7
C . 6 a 7
D . 3 a 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC a. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC). Tính để thể tích khối chóp S.ABC lớn nhất
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC = a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Tính để thể tích khối chóp S.ABC lớn nhất
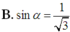
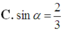
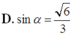
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB 2a, góc giữa (SBC) và mặt đáy bằng
60
0
. Thể tích khối chóp S.ABC là:
A
.
125
2
a
3
6
B
.
3
6...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với (ABC), tam giác ABC là tam giác vuông cân tại A, AB = 2a, góc giữa (SBC) và mặt đáy bằng 60 0 . Thể tích khối chóp S.ABC là:
A . 125 2 a 3 6
B . 3 6 a 3 4
C . 16 2 a 3 3
D . 2 6 a 3 3