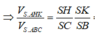Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB a
10
, BC 2a, SC 2a
3
. Thể tích khối chóp S.ABC là:
A
.
3
a
3
2
B
.
3
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Biết SA vuông góc với mặt phẳng đáy và SB = a 10 , BC = 2a, SC = 2a 3 . Thể tích khối chóp S.ABC là:
A . 3 a 3 2
B . 3 a 3 2
C . 3 a 3
D . a 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết Tính thể tích V của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết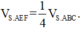 
Tính thể tích V của khối chóp S.ABC
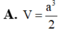
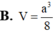
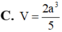
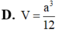
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB a, BC a
3
Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng
5
a
2
3
2
. Tính theo a khoảng cách d từ A đến mặt...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB =a, BC =a 3 Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72a
B. 0,9a
C. 0,8a
D. 1,12a
Cho hình chóp S.ABC có SC 2a,
S
C
⊥
(
A
B
C
)
Đáy ABC là tam giác vuông cân tại B và có
(
α
)
Mặt phẳng
(
α
)
đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE. A.
4...
Đọc tiếp
Cho hình chóp S.ABC có SC= 2a, S C ⊥ ( A B C ) Đáy ABC là tam giác vuông cân tại B và có ( α ) Mặt phẳng ( α ) đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE.
A. 4 a 3 9
B. 2 a 3 3
C. 2 a 3 9
D. a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB AC a
3
và góc
A
B
C
^
30
0
.Biết SA vuông góc với mặt phẳng đáy và SC 2a. Thể tích hình chóp là:
A
.
3
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB = AC = a 3 và góc A B C ^ = 30 0 .Biết SA vuông góc với mặt phẳng đáy và SC = 2a. Thể tích hình chóp là:
A . 3 a 3 3 4
B . a 3 3 4
C . a 3 3 2
D . 3 a 3 3 2
Cho hình chóp S.ABCD có SA vuông góc với đáy. Mặt phẳng (a) qua A vuông góc với SC tại H. cắt SB, SD lần lượt tại 1 và K. Mặt phẳng qua I, K song song với SC cắt các cạnh BC,CD lần lượt tại E và F. Biết SC hợp với đáy một góc 60°. Tính diện tích tứ giác AECF, biết diện tích tứ giác AIHK bằng 10.A. 12√3.B. 20√3 3C. 8√3 3D. 4√3.
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với đáy. Mặt phẳng (a) qua A vuông góc với SC tại H. cắt SB, SD lần lượt tại 1 và K. Mặt phẳng qua I, K song song với SC cắt các cạnh BC,CD lần lượt tại E và F. Biết SC hợp với đáy một góc 60°. Tính diện tích tứ giác AECF, biết diện tích tứ giác AIHK bằng 10.
A. 12√3.
B. 20√3 3
C. 8√3 3
D. 4√3.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Biết rằng AB a, AC a
3
và
S
B
A
^
60
0
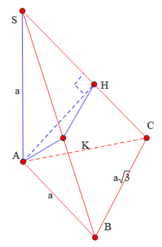
. Gọi H là hình chiếu vuông góc của A trên cạnh SC. Tính tỷ số thể tích của hai khối SABH và HABC.
A
.
3
4...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Biết rằng AB = a, AC = a 3 và S B A ^ = 60 0 . Gọi H là hình chiếu vuông góc của A trên cạnh SC. Tính tỷ số thể tích của hai khối SABH và HABC.
A . 3 4
B . 1 12
C . 3 2
D . 7 4
Cho khối chóp S.ABC có đáy là tam giác vuông tại A SB
⊥
(
A
B
C
)
,
A
B
a
,
A
C
B
^
30
0
, góc...
Đọc tiếp
Cho khối chóp S.ABC có đáy là tam giác vuông tại A SB
⊥ ( A B C ) , A B = a , A C B ^ = 30 0 , góc giữa đường thẳng SC và mặt phẳng (ABC) là 60°. Tính thể tích V của khối chóp S.ABC theo a.
A. V= 3 a 3
B. V= a 3
C. V= 2 a 3
D. V= 3 a 3 2
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng (α) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, AC, SD tại B', C', D'. Chứng minh B'D' song song với BD và AB' vuông góc với SB.