rút gọn biểu thức sau:
B=x.y
biết: (3a3-3b3)x-2b=2a và (4a+4b)y=9
Rút gọn biểu thức: P = xy , biết ( 3 a 3 − 3 b 3 ) x − 2 b = 2 a với a ≠ b và ( 4 a + 4 b ) y = 9 ( a − b ) 2 với
Biến đổi được: x = 2 ( a + b ) 3 ( a 3 − b 3 ) ; y = 9 ( a − b ) 2 4 ( a + b )
⇒ P = x . y = 2 ( a + b ) 3 ( a 3 − b 3 ) . 9 ( a − b ) 2 4 ( a + b ) = 3 ( a − b ) 2 ( a 2 + ab + b 2 )
\(A=\left(\dfrac{1}{2a-b}-\dfrac{a^2-1}{2a^3-b+2a-a^2b}\right)\div\left(\dfrac{4a+2b}{a^3b+ab}-\dfrac{2}{a}\right)\)
a) rút gọn biểu thức A
b)tính giá trị biểu thức A biết 4a^2+b^2=5ab a>b>0
Rút gọn các biểu thức sau (với a và b không âm):
a ) √ ( 3 a 3 ) . √ 12 a = √ ( 3 a 3 . 12 a ) = √ ( 36 a 4 )
b ) √ ( 2 a . 32 a b 2 ) = √ ( 64 a 2 b 2 )
a ) √ ( 3 a 3 ) . √ 12 a = √ ( 3 a 3 . 12 a ) = √ ( 36 a 4 ) = √ ( ( 6 a 2 ) 2 ) = 6 a 2 ( d o a 2 ≥ 0 ) b ) √ ( 2 a . 32 a b 2 ) = √ ( 64 2 b 2 ) = √ ( ( 8 a b ) 2 ) = 8 a b ( d o a ≥ 0 ; b ≥ 0 )
M=(2/2a-b + 6b/b^2 - 4a^2 - 4/2a+b) : (1+ 4a^2+4b^2/4a^2-b^2)
a) Rút gọn biểu thức M
b) Tính giá trị biểu thức M khi a=1/3 và b=2
Viết rõ đề bài ra đc không ạ
Bài làm:
a) đkxđ: \(2a\ne\pm b\)
Ta có: \(M=\left(\frac{2}{2a-b}+\frac{6b}{b^2-4a^2}-\frac{4}{2a+b}\right)\div\left(\frac{1+4a^2+4b^2}{4a^2-b^2}\right)\)
\(M=\left[\frac{2\left(2a+b\right)-6b-4\left(2a-b\right)}{\left(2a-b\right)\left(2a+b\right)}\right].\left(\frac{\left(2a-b\right)\left(2a+b\right)}{4a^2+4b^2+1}\right)\)
\(M=\frac{4a+2b-6b-8a+4b}{4a^2+4b^2+1}\)
\(M=\frac{-4a}{4a^2+4b^2+1}\)
b) +Nếu: \(a=\frac{1}{3}\)và \(b=2\)
Khi đó GT của M là: \(M=\frac{-4.\frac{1}{3}}{4.\frac{1}{3^2}+4.2^2+1}=-\frac{12}{157}\)
Viết rõ đề ra nhá
Thu gọn biểu thức sau
a) 3a + 4b - 5c - 2a - 3b + 5c
b) 7a + 3b - 4c - 3a+ 2b - 2c - 4a + b - 2c
a) 3a + 4b - 5c - 2a - 3b + 5c
= ( 3a - 2a ) + ( 4b - 3b ) - ( 5c - 5c )
= a + b
b) 7a + 3b - 4c - 3a + 2b - 2c - 4a + b - 2c
= ( 7a - 3a - 4a ) + ( 3b + 2b + b ) - ( 4c + 2c + 2c )
= 6b - 8c
a) 3a + 4b - 5c - 2a - 3b + 5c
= (3a - 2a) + (4b - 3b) - (5c - 5c)
= a + b - 0 = a + b
b) 7a + 3b - 4c - 3a + 2b - 2c - 4a + b - 2c
= (7a - 3a - 4a) + (3b + 2b + b) - ( 4c + 2c + 2c)
= 0 + 6b - 8c = 6b - 8c
a)
3a + 4b - 5c - 2a - 3b + 5c
=( 3a - 2a ) + ( 4b - 3b ) + ( -5c + 5c )
= a + b
b)
7a + 3b - 4c - 3a + 2b - 2c - 4a + b - 2c
=( 7a - 3a - 4a ) + ( 3b + 2b + b ) + ( -4c - 2c - 2c )
= 6b + (-8c)
rút gọn biểu thức :
(2a - 3b) - (5b - d) + (8b - d) = 2a
(a + b ) - (d - 4b ) - (c - 10d) = 2a - 2b - 6d +c
(2a-3b)-(5b-d)+(8b-d)
\(=2a-3b-5b+d+8b-d\)
\(=2a+\left(8b-3b-5b\right)+\left(d-d\right)\)
=2a
\(\left(a+b\right)-\left(d-4b\right)-\left(c-10d\right)\)
\(=a+b-d+4b-c+10d\)
\(=a+5b+11d-c\)
Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số): 4 a 2 - 9 x = 4 a + 4 ; với a ≠ ± 3/2 và 3 a 3 + 3 y = 6 a 2 + 9 a với a ≠ - 1
Vì a
≠
±
3/2 nên
4
a
2
-
9
≠
0 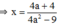
Vì a
≠
- 1 nên
3
a
3
+
3
≠
0 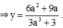
Do đó: 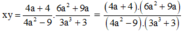
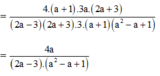
Cho biểu thức sau:
\(P=\left(\frac{1}{ab-2}+\frac{1}{ab+2}+\frac{2ab}{a^2b^2+4}+\frac{4a^3b^3}{a^4b^4+16}\right).\frac{a^4b^4+16}{a^4b^4}\)
a, Rút gọn biểu thức P
b, Tính giá trị của P khi \(\frac{a^2+4}{b^2+9}=\frac{a^2}{9}\)
ĐKXĐ : \(\hept{\begin{cases}ab-2\ne0\\ab+2\ne0\\a^4b^4\ne0\end{cases}}\Rightarrow ab\ne\pm2;a\ne0;b\ne0\)
\(P=\left(\frac{1}{ab-2}+\frac{1}{ab+2}+\frac{2ab}{a^2b^2+4}+\frac{4a^3b^3}{a^4b^4+16}\right).\frac{a^4b^4+16}{a^4b^4}\)
\(=\left(\frac{2ab}{a^2b^2-4}+\frac{2ab}{a^2b^2+4}+\frac{4a^3b^3}{a^4b^4+16}\right).\frac{a^4b^4+16}{a^4b^4}\)
\(=\left(\frac{4a^3b^3}{a^4b^4-16}+\frac{4a^3b^3}{a^4b^4+16}\right).\frac{a^4b^4+16}{a^4b^4}\)
\(=\frac{8a^5b^5}{a^8b^8-16^2}.\frac{a^4b^4+16}{a^4b^4}=\frac{8a^5b^5\left(a^4b^4+16\right)}{\left(a^4b^4-16\right)\left(a^4b^4+16\right).a^4b^4}\)
\(=\frac{8ab}{a^4b^4-16}\)
b) Khi \(\frac{a^2+4}{b^2+9}=\frac{a^2}{9}\)
=> (a2 + 4).9 = a2(b2 + 9)
=> 9a2 + 36 = a2b2 + 9a2
=> a2b2 = 36
=> (ab)2 = 36
=> \(\orbr{\begin{cases}ab=6\left(tm\right)\\ab=-6\left(tm\right)\end{cases}}\)
Khi ab = 6 => P = \(\frac{8ab}{\left(ab\right)^4-16}=\frac{8.6}{6^4-16}=\frac{48}{1280}=\frac{3}{80}\)
Khi ab = -6 => P = \(\frac{8ab}{\left(ab\right)^4-16}=\frac{8.\left(-6\right)}{\left(-6\right)^4-16}=-\frac{3}{80}\)
Rút gọn các biểu thức sau a)(căn1-4a+4a^2 ) -2a b)x-2y-căn x^2-4xy+4y^2
a) \(\sqrt[]{1-4a+4a^2}\)
\(=\sqrt[]{\left(1-2a\right)^2}\)
\(=\left|1-2a\right|\)
\(=\left[{}\begin{matrix}1-2a\left(a\le\dfrac{1}{2}\right)\\2a-1\left(a>\dfrac{1}{2}\right)\end{matrix}\right.\)
b) \(x-2y-\sqrt[]{x^2-4xy+4y^2}\)
\(=x-2y-\sqrt[]{\left(x-2y\right)^2}\)
\(=x-2y-\left|x-2y\right|\)
\(=\left[{}\begin{matrix}x-2y-x+2y\left(x\ge2y\right)\\x-2y+x-2y\left(x< 2y\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}0\left(x\ge2y\right)\\2x-4y\left(x< 2y\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}0\left(x\ge2y\right)\\2\left(x-2y\right)\left(x< 2y\right)\end{matrix}\right.\)
Cho biểu thức: A=\(\left(\frac{1}{2a+b}-\frac{a^2-1}{2a^3-b+2a-a^2b}\right)\times\)\(\left(\frac{4a+2b}{a^3b+ab}-\frac{2}{a}\right)\)
a) Rút gọn A
b) Tính giá trị A biết 4a2+b2= 5ab và a>b>0
Sửa lại đề bài: 1 / 2a- b
( MÁY MK KO ĐÁNH ĐC PHÂN SỐ MONG BN THÔNG CẢM)
mới lm đc nhé bn!
a) ĐKXĐ: bn tự lm nhé !
bn biến đổi: 2a3-b+2a-a2b = (2a-b) + ( 2a3-a2b) = (2a-b) + a2(2a-b) = (2a-b)(a2+1)
rồi bn nhân 1 / 2a+b với a2+1 rồi trừ 2 phân thức với nhau sẽ ra 0 => A=0