Cho hình chữ nhật MNPQ.Gọi O là giao điểm của 2 đường chéo.Tính các góc của tam giác MNP biết góc MOQ=50o

Những câu hỏi liên quan
Cho Hình chữ nhật ABCD . Gọi O là giao điểm của 2 đường chéo.Tính các góc của Tam giác ABD , biết góc ABD =50°
Xem chi tiết
Cho hình chữ nhật ABCD.Gọi O là giao điểm của hai đường chéo.Tính các góc của tam giác ABD,biết góc AOD=40 độ
AOD = 40 => AOB = 140
vì tam giác AOB cân tại O (theo tính chất hình chữ nhật)
=> OAB = OBA = 20
vì O thuộc DB
=> ABO = ABD = 20
k tui nha
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD (AD<AB).Từ B,kẻ đường thẳng vuông góc với BD cắt DC tại E.Gọi K là giao điểm các đường phân giác các góc trong của tam giác BCD,gọi G là giao điểm các đường phân giác các góc trong của tam giác BCE.Đường thẳng KG cắt BD và BE theo thứ tự tại M và N.CM; MN^2=2CD*CE
Cho tam giác MNP vuông tại M, đường cao a) Biết . Tính MH, MN, MP (độ dài đoạn thẳng chỉ dùng ở câu a)b) Kẻ HD vuông góc với MN tại D, HE vuông góc với MP tại E. Gọi O là giao điểm của MH và DE. Chứng minh: MDHE là hình chữ nhật và MH DEc) Chứng minh: và NH 14,4 Ph25,6d) Chứng minh: e) Chứng minh: g) Qua E kẻ EQ DE Chứng minh Q là trung điểm PH và O là trực tâm của tam giác MNQ
Đọc tiếp
Cho tam giác MNP vuông tại M, đường cao
a) Biết .
Tính MH, MN, MP (độ dài đoạn thẳng chỉ dùng ở câu a)
b) Kẻ HD vuông góc với MN tại D, HE vuông góc với MP tại E. Gọi O là giao điểm của MH và DE. Chứng minh: MDHE là hình chữ nhật và MH = DE
c) Chứng minh: và NH 14,4 Ph25,6
d) Chứng minh:
e) Chứng minh:
g) Qua E kẻ EQ DE
Chứng minh Q là trung điểm PH và O là trực tâm của tam giác MNQ
a) Vì tam giác MNP vuông tại M, nên MN là đường cao của tam giác và MH là đường trung tuyến. Do đó, MH = MN/2. Với giá trị của MN đã biết, bạn có thể tính được MH.
b) Khi kẻ HD vuông góc với MN tại D và HE vuông góc với MP tại E, ta có MDHE là hình chữ nhật. Vì MH là đường trung tuyến của tam giác MNP, nên MH = DE theo tính chất của đường trung tuyến.
c) Để chứng minh NH = 14,4 và PH = 25,6, chúng ta cần biết thêm thông tin về tam giác MNP hoặc các giá trị khác liên quan. Xin lỗi vì không thể giúp bạn với câu hỏi này vì thiếu thông tin.
d) Để chứng minh , chúng ta cần biết thêm thông tin về tam giác MNP hoặc các giá trị khác liên quan. Xin lỗi vì không thể giúp bạn với câu hỏi này vì thiếu thông tin.
e) Để chứng minh , chúng ta cần biết thêm thông tin về tam giác MNP hoặc các giá trị khác liên quan. Xin lỗi vì không thể giúp bạn với câu hỏi này vì thiếu thông tin.
g) Để chứng minh O là trực tâm của tam giác MNQ, chúng ta cần biết thêm thông tin về tam giác MNP hoặc các giá trị khác liên quan. Xin lỗi vì không thể giúp bạn với câu hỏi này vì thiếu thông tin.
Đúng 1
Bình luận (0)
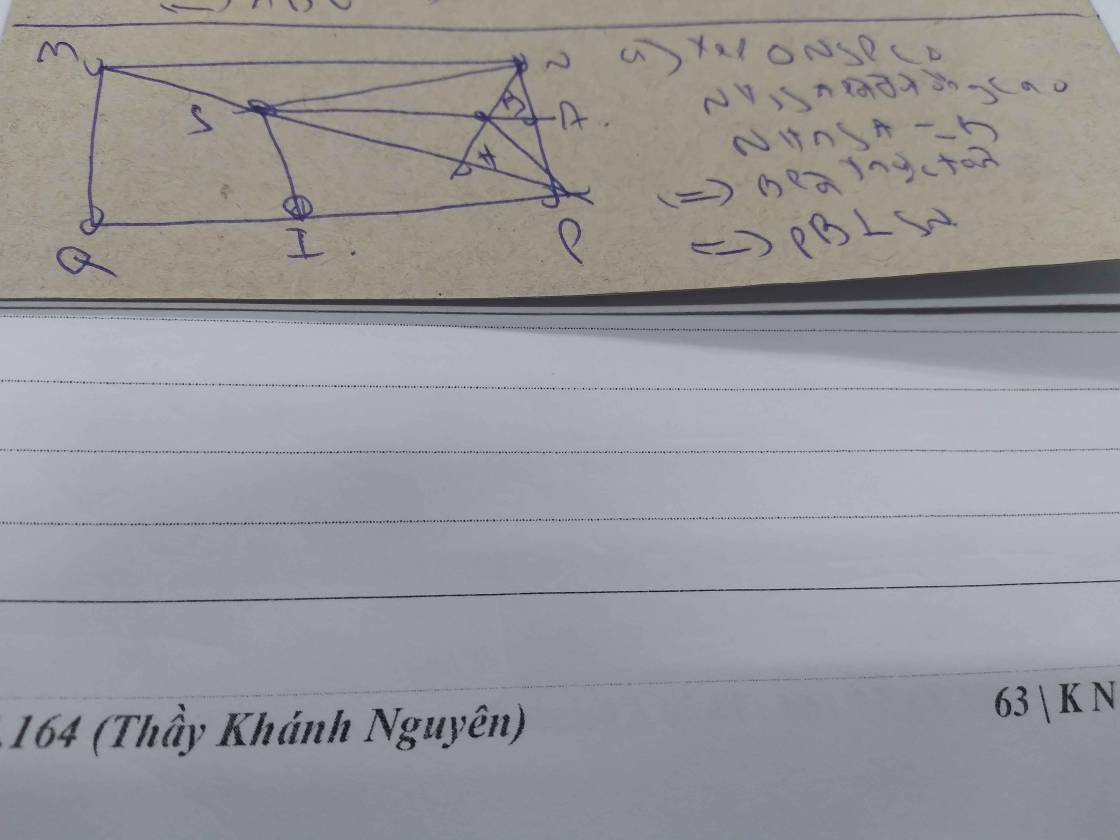
Bài4:Cho hình chữ nhật MNPQ.Gọi S là một điểm thuộc đoạn MP.Trong tam giác NSP,hai đường cao SA và NH cắt nhau ởB.Đường thẳng qua S vuông góc với SN cắt PQ ở I. a)Chứng minh:PB vuông góc với SN và tứ giác SBPI là hình bình hành. b)Chứng minh tam giác BSH đồng dạng với tam giác MQP. c)Gỉa sử S là trung điểm của MH chứng minh: 2.BN.PI-SH.MQ.
tứ giác ABCD có AB=BC=CD,góc A+góc D=140o.Gọi O là giao điểm của hai đường chéo.Tính góc AOD
Mn giúp mk bài này vs ạBài toán 1: Cho tam giác ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm 0 cách đều 3 đỉnh của tam giác ABC. Bài toán 2: Cho tam giác cân ABC (AB AC). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.Bài toán 3: Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM BN CP.a) Chứng minh tam giác MNP là tam giác đều b) Gọi O là giao điểm các đư...
Đọc tiếp
Mn giúp mk bài này vs ạ
Bài toán 1: Cho tam giác ABC cân tại A, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm 0 cách đều 3 đỉnh của tam giác ABC.
Bài toán 2: Cho tam giác cân ABC (AB = AC). Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của góc ACB. Tính các góc của tam giác ABC.
Bài toán 3: Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM = BN = CP.
a) Chứng minh tam giác MNP là tam giác đều b) Gọi O là giao điểm các đường trung trực của tam giác ABC. Chứng minh rằng 0 cũng là
giao điểm của các đường trung trực của tam giác MNP.
im đi Lê Minh Phương
kệ mẹ tao, thằng điên
Xem thêm câu trả lời
Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP. Chứng minh
a) Tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA
a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
Do đó: MDHE là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M (MN<MP). Gọi I là trung điểm của NP. Vẽ IH vuông góc với MN tại H, IK vuông góc với MP tại K. E là điểm đối xứng của I qua K. Kẻ đường cao AH. Biết tứ giác MHIK là hình chữ nhật, tứ giác MIPE là hình thoi. Chứng minh tứ giác HAIK là hình thang cân.