Cho hệ :
x2 + y2 = a2 +2a -3
x+y = 2a-1
Tìm điều kiện của a để hệ đã cho có nghiệm với giá trị nào của a thì hệ có nghiệm (x,y) thêm xy đạt giá trị nhỏ nhất
Những câu hỏi liên quan
Cho hệ phương trình
x
+
y
2
a
+
1
x
2
+
y...
Đọc tiếp
Cho hệ phương trình x + y = 2 a + 1 x 2 + y 2 = a 2 - 2 a + 3 .Giá trị của tham số a sao cho hệ có nghiệm (x;y) và tích x.y nhỏ nhất là:
A. a = 1
B. a = - 1
C. a = 2
D. a = - 2
11 tháng 1 2022 lúc 20:02
Cho hệ phương trình \(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\) (với m là tham số)
Tìm m để hệ đã cho có nghiệm (x;y) thỏa mãn: x2 + y2 + 3 đạt giá trị nhỏ nhất.
\(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y+x+2y=4m-2+3m+2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\m+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\2y=2m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m+1\end{matrix}\right.\)
\(x^2+y^2+3\\ =m^2+\left(m+1\right)^2+3\\ =m^2+m^2+2m+1+3\\ =2m^2+2m+4\\ =2\left(m^2+m+2\right)\)
\(=2\left(m^2+m+\dfrac{1}{4}+\dfrac{7}{4}\right)\)
\(=2\left[\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\right]\)
\(=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy ...
Đúng 1
Bình luận (0)
Cho hệ phương trình \(\left\{{}\begin{matrix}2x+y=3m-5\\x-y=2\end{matrix}\right.\)(m là tham số)
a, giải hệ phương trình với m=2
b, gọi nghiệm của hệ là (x;y), tìm giá trị của m để x2+y2 đạt giá trị nhỏ nhất
a, Thay m = 2 ta được \(\left\{{}\begin{matrix}2x+y=1\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
b, \(\Leftrightarrow\left\{{}\begin{matrix}3x=3m-3\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m-1\\y=m-3\end{matrix}\right.\)
Ta có : \(x^2+y^2=m^2-2m+1+m^2-6m+9=2m^2-8m+10\)
\(=2\left(m^2-4m+4-4\right)+10=2\left(m-2\right)^2+2\ge2\forall m\)
Dấu''='' xảy ra khi m =2
Vậy ...
Đúng 4
Bình luận (0)
Cho phương trình: x2-(2a-1)x-4a-3=0
a)CMR: phương trình luôn có nghiệm với mọi giá trị của a
b) Tìm hệ thức liên hệ giữa 2 nghiệm x1,x2 không phụ thuộc vào a
c) Tìm giá trị nhỏ nhất của biểu thức A=x12+x22
\(x^2-\left(2a-1\right)x-4a-3=0\)
\(\Delta=\left(2a-1\right)^2+4\left(4a+3\right)\)
\(=4a^2-4a+1+16a+12\)
\(=4a^2+12a+13=\left(2a+3\right)^2+4>0\)
Vì \(\Delta>0\Rightarrow\) phương trình có 2 nghiệm phân biệt với mọi a
Vì phương trình có 2 nghiệm phân biệt, áp dụng hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2a-1\\x_1.x_2=-4a-3\end{matrix}\right.\) ⇒ \(x_1.x_2+2\left(x_1+x_2\right)=-5\)
Ta có:
\(A=x_1^2+x^2_2=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=\left(2a-1\right)^2-2\left(-4a-3\right)\)
\(=4a^2-4a+1+8a+6\)
\(=\left(2a+1\right)^2+6\)
Vì \(\left(2a+1\right)^2\ge0\forall a\)
⇒\(A\ge6\)
Min A=6 <=> \(a=-\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Biết cặp số (x; y) là nghiệm của hệ
x
+
y
2
m
x
2
+
y
2
2
m...
Đọc tiếp
Biết cặp số (x; y) là nghiệm của hệ x + y = 2 m x 2 + y 2 = 2 m + 2 . Tìm giá trị của m để P = xy – 3 (x + y) đạt giá trị nhỏ nhất.
A. m = - 7 2
B. m = −7
C. m = 7
D. m = 7 2
Cho hệ phương trình:
k
x
+
y
7
2
x
-
y
-
4
Gọi (x; y) là nghiệm của hệ phương trình . Xác định giá trị của k để P
x
2
+...
Đọc tiếp
Cho hệ phương trình:
k x + y = 7 2 x - y = - 4
Gọi (x; y) là nghiệm của hệ phương trình . Xác định giá trị của k để P = x 2 + y 2 đạt giá trị nhỏ nhất.
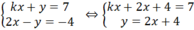
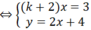
Với k + 2 ≠ 0 ⇔ k ≠ -2 thì hệ phương trình có nghiệm :
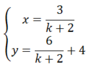
Ta có:
P = x 2 + y 2 = x 2 + 2 x + 4 2
= 5 x 2 + 16 x + 16
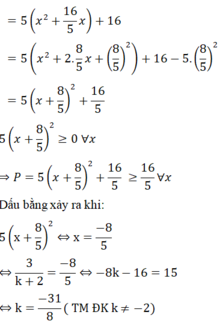
Vậy với k = (-31)/8 thì biểu thức P = x 2 + y 2 đạt giá trị nhỏ nhất
Đúng 0
Bình luận (0)
Với giá trị nào của a thì hệ phương trình
x
+
y
1
x
-
y
2
a
-
1
có nghiệm (x;y) với x.y lớn nhất? A. ...
Đọc tiếp
Với giá trị nào của a thì hệ phương trình x + y = 1 x - y = 2 a - 1 có nghiệm (x;y) với x.y lớn nhất?
A. a = 1 4
B. a = 1 2
C. a = - 1 2
D. a = 1
Ta có : x + y = 1 x - y = 2 a - 1 ⇔ x + y = 1 2 x = 2 a ⇔ y = 1 - a x = a
Do đó :
x y = a . 1 - a = a - a 2 = - a 2 - 2 . 1 2 a + 1 4 + 1 4 = - a - 1 2 2 + 1 4
Do - a - 1 2 2 ≤ 0 ∀ a ⇒ - a - 1 2 2 + 1 4 ≤ 1 4
Suy ra,giá trị lớn nhất của xy là 1 4 khi a = 1 2 .
Đáp án là B.
Đúng 0
Bình luận (0)
Với giá trị nào của m thì hệ phương trình
{(m+1)x - y = m+1
{x + (m+1)y = 2
Có nghiệm thoả mãn điều kiện S=x+y đạt giá trị nhỏ nhất
Biết cặp số (x; y) là nghiệm của hệ
x
+
y
m
x
2
+
y
2
-
m
2...
Đọc tiếp
Biết cặp số (x; y) là nghiệm của hệ x + y = m x 2 + y 2 = - m 2 + 6 . Tìm giá trị của m để P = xy + 2(x + y) đạt giá trị nhỏ nhất.
A. m = −1
B. m = −2
C. m = 1
D. m = 0
