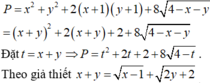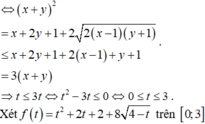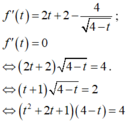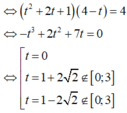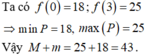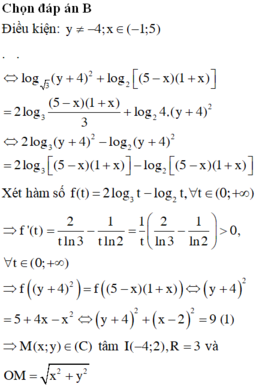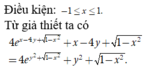Cho 2 số x, y thỏa mãn 2(x2+y2) =2025. giá trị lớn nhất của x+ y là bao nhiêu

Những câu hỏi liên quan
Cho 2 số x, y thỏa mãn 2(x^2+y^2) =2025. giá trị lớn nhất của x+ y là bao nhiêu.
Cho hai số thực x, y thỏa mãn
x
2
+
y
2
-
4
x
+
6
y
+
4
+
y
2
+
6
y
+
10
6
+
4
x
-
x
2...
Đọc tiếp
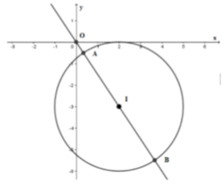
Cho hai số thực x, y thỏa mãn x 2 + y 2 - 4 x + 6 y + 4 + y 2 + 6 y + 10 = 6 + 4 x - x 2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T = x 2 + y 2 - a . Có bao nhiêu giá trị nguyên thuộc đoạn [-10;10] của tham số a để M ≥ 2 m
A. 17
B. 16
C. 15
D. 18
Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
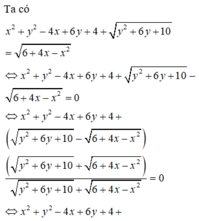
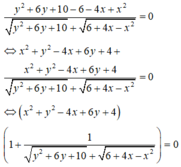


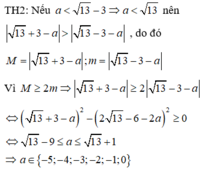

Đúng 0
Bình luận (0)
Cho x, y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của
P
x
2
+
y
2
+
2
(
x
+
1
)
(
y
+
1
)
+
8
4
-
x
-...
Đọc tiếp
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43
Cho x , y là các số thực thỏa mãn
x
+
y
x
-
1
+
2
y
+
2
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
2...
Đọc tiếp
Cho x , y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y . Khi đó, giá trị của M+m bằng.
A. 41
B. 42
C. 43
D. 44
Cho 2 số thực x ; y thỏa mãn 0 < x ≤ 1 , 0 < y ≤ 1 và x + y = 3xy . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x2 + y2 - 4xy
Cho hai số x,y \(\ge\)0 thay đổi và thỏa mãn x+y=2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P= x(x3 + x2 + x + 1004y) + y(y3 + y2 + y +1004x) + 1
Cho hai số thực x, y thỏa mãn:
log
3
(
y
2
+
8
y
+
16
)
+
l
o
g
2
[(
5
−
x
)
(
1
+
x
)
]2log
3
5
+
4
x...
Đọc tiếp
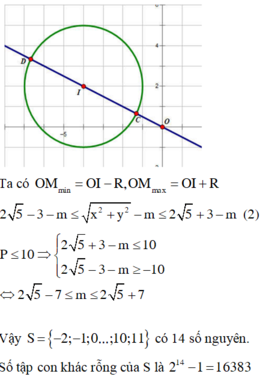
Cho hai số thực x, y thỏa mãn: log 3 ( y 2 + 8 y + 16 ) + l o g 2 [( 5 − x ) ( 1 + x ) ]=2log 3 5 + 4 x − x 2 3 + log 2 ( 2 y + 8 ) 2 . Gọi S là tập các giá trị nguyên của tham số m để giá trị lớn nhất của biểu thức P = x 2 + y 2 − m không vượt quá 10. Hỏi S có bao nhiêu tập con không phải là tập rỗng?
A. 2047
B. 16383
C. 16384
D. 32
Cho hai số thực x, y thỏa mãn
x
2
-
y
2
+
1
2
+
4
x
2
y
2
-
x
2
-
y
2
0
. Gọi...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 - y 2 + 1 2 + 4 x 2 y 2 - x 2 - y 2 = 0 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x 2 + y 2 . Tính M + m
A. M + m = 3
B. M + m = 5
C. M + m = 2
D. M + m = 4
Cho 2 hai số thực x, y thỏa mãn
e
x
-
4
y
+
1
-
x
2
-
e
y
2
+
1
-
x...
Đọc tiếp
Cho 2 hai số thực x, y thỏa mãn e x - 4 y + 1 - x 2 - e y 2 + 1 - x 2 - y = y 2 - x 4 . Giá trị lớn nhất của biểu thức P = x 3 + 2 y 2 - 2 x 2 + 8 y - x + 2 bằng
A. 2
B. 58 27
C. 115 27
D. 122 27