Giúp mik với
a.Chứng minh Ax//Cz

b)Chứng minh Ma//Kb,NC//KB.Tính góc MNC,CNK

cho tam giác abc vuông tại a có m là trung điểm bc. trên tia đối ma lấy điểm n sao cho ma=mn
a chứng minh: NC vuông góc AC
b Tính CNA , Biết ABC=37
giúp mik vs mik đang cần gắp
a: Xét tứ giác ABNC có
M là trung điểm của BC
M là trung điểm của AN
Do đó: ABNC là hình bình hành
Suy ra: AB//NC
hay NC⊥AC
b: Xét tứ giác ACNB có
\(\widehat{CAB}+\widehat{CNB}=180^0\)
nên ACNB là tứ giác nội tiếp
Suy ra: \(\widehat{CNA}=\widehat{ABC}=37^0\)
1,Cho tam giác ABC có góc BAC = 80 độ . Kẻ Ax là tia phân giác của góc BAC ; Ax cắt BC tại M, Trên cạnh AC lấy điểm N sao cho AMN = 40 độ
a, Chứng minh MN // BA
b,Tính số đo góc ANM
c,Từ N kẻ tia Ny // Ax |Ny nằm trong góc MNC | , Chứng minh Ny là tia phân giác của góc MNC
Cho ∆ ABC có BC = 2AB , M là trung điểm của BC . Kẻ BH vuông góc với AM, CK vuông góc với AM. a, Chứng minh: AH = HM = MK b, Từ M kẻ đường thẳng song song với AB , cắt CK ở N . Chứng minh: ∆ MNC cân . ( Mn làm gấp giúp mik bài này với , mai mik kiểm tra r)
Bổ sung thêm ý c là : Chứng minh: HK = AM và BN vuông góc với NC
Bài tập : cho tam giác ABC có góc BAC = 80 độ . Kẻ Ax là tia phân giác góc BAC; Ax cắt BC tại M . Trên cạnh AC lấy điểm N sao cho góc AMN = 40 độ
a] Chứng minh MN// BA b] Tính số đo góc ANM
c] Từ N kẻ tia Ny // Ax { Ny nằm trong góc MNC }. Chứng minh Ny là tia phân giác góc MNC.
Các bạn giúp mình kẻ hình và giải nhé! Cảm ơn các bạn trước
a) Vì tia Ax là tia phân giác của \(\widehat{BAC}\)
\(\widehat{BAx}\) = \(\widehat{xAC}\) = \(\frac{\widehat{ABC}}{2}\) = \(\frac{80^0}{2}\) = 40*
=> \(\widehat{BAM}\) = \(\widehat{AMN}\) = 40*
=> MN // BA
b, Có: góc AMN + góc ANM + góc NAM = 180 độ
=> góc ANM = 180 độ - (góc AMN + góc NAM) = 180 độ - 80 độ = 100 độ
c, Vì Ax // Ny => góc AMN = góc MNy = 40 độ (so le trong)
=> góc xAN = góc yNC = 40 độ (đồng vị)
Vì góc MNy = góc yNC = 40 độ và Ny nằm giữa MN và NC
=> Ny là tia phân giác của góc MNC
cam on 2 ban ca hai cai deu dung nhung mk chi duoc bam dung 1 lan
Bài tập : cho tam giác ABC có góc BAC = 80 độ . Kẻ Ax là tia phân giác góc BAC; Ax cắt BC tại M . Trên cạnh AC lấy điểm N sao cho góc AMN = 40 độ
a] Chứng minh MN// BA b] Tính số đo góc ANM
c] Từ N kẻ tia Ny // Ax { Ny nằm trong góc MNC }. Chứng minh Ny là tia phân giác góc MNC.
Các bạn giúp mình kẻ hình và giải nhé! Cảm ơn các bạn trước
Bài tập : cho tam giác ABC có góc BAC = 80 độ . Kẻ Ax là tia phân giác góc BAC; Ax cắt BC tại M . Trên cạnh AC lấy điểm N sao cho góc AMN = 40 độ
a] Chứng minh MN// BA b] Tính số đo góc ANM
c] Từ N kẻ tia Ny // Ax { Ny nằm trong góc MNC }. Chứng minh Ny là tia phân giác góc MNC.
Các bạn giúp mình kẻ hình và giải nhé! Cảm ơn các bạn trước
Cho tam giác MNC (MN < NC) Gọi A là trung điểm của MC. Trên tia đối của tia AN lấy điểm B sao cho AB = AN a) Chứng minh: tam giác AMN = tam giác ACB b) Chứng minh: MN // BC. c) Kẻ MD vuông góc với BN tại D, kẻ CE vuông góc với BN tại F. Chứng minh IE = CD
Vẽ hình và làm bài giúp, cảm ơn ạ!
a: Xét ΔAMN và ΔACB có
AM=AC
\(\widehat{MAN}=\widehat{CAB}\)(hai góc đối đỉnh)
AN=AB
Do đó: ΔAMN=ΔACB
b: Ta có: ΔAMN=ΔACB
=>\(\widehat{AMN}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NM//BC
c: Sửa đề: ME=CD
Xét ΔMDA vuông tại D và ΔCEA vuông tại E có
AM=AC
\(\widehat{MAD}=\widehat{CAE}\)(hai góc đối đỉnh)
Do đó: ΔMDA=ΔCEA
=>DA=EA
Xét ΔMAE và ΔCAD có
AM=AC
\(\widehat{MAE}=\widehat{CAD}\)(hai góc đối đỉnh)
AE=AD
DO đó:ΔMAE=ΔCAD
=>ME=CD
Tam giác ABC, MA=MB, NA=NC. CM cắt Bn tại G; AG cắt BC tại K. Chứng minh KB = KC.
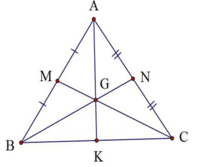
Theo bài ra ta có diện tích ABG=ACG; Vì hai tam giác ABG và ACG có cạnh AG chung nên đường cao hạ từ B và đường cao hạ từ C sẽ bằng nhau ( *)
- Xét tam giác BGK và CGK có cạnh GK chung và từ (*) ta có đường cao hạ từ B và C bằng nhau. Do đó: Diện tích BGK và CGK bằng nhau (**)
Mặt khác ta thấy: hai tam giác BGK và CGK có chung đường cao hạ từ G (***)
- Từ ( **) và (***) ta có KB=KC ( đpcm)
Bạn nào vẽ hình giúp mik vs.
Cho nửa đường tròn đường kính AB.Kẻ tia Ax vuông góc với AB.Trên Ax lấy điểm M.Qua M,kẻ tiếp tuyến MN với nửa đường tròn.Chứng minh MN=MA
Xét (O) có
MN là tiếp tuyến có N là tiếp điểm
MA là tiếp tuyến có A là tiếp điểm
Do đó: MN=MA