cho hàm số f(f(x)+2y)=4x+4y+3 với mọi số thực x, y. Tìm f(x)

Những câu hỏi liên quan
Cho hàm số y=f(x)=4x² - 5
a) Tính f(3), f(-1/2)
b) Tìm x để f(x) = -1
c)Chứng tỏ với mọi x ∈ R thì f(x)= f(-x)
Giúp mình với ạ cẻm ưn nhiều:3
a) Ta có: \(y=f\left(x\right)=4x^2-5\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(3\right)=4.3^2-5=31\\f\left(-\dfrac{1}{2}\right)=4.\left(-\dfrac{1}{2}\right)^2-5=-4\end{matrix}\right.\)
b) Ta có: \(f\left(x\right)=-1\)
\(\Rightarrow4x^2-5=-1\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\) thì \(f\left(x\right)=-1\)
c) \(\forall x\in R,f\left(x\right)=f\left(-x\right)\Leftrightarrow f\left(-x\right)=4.\left(-x\right)^2-5=4x^2-5=f\left(x\right)\)
Vậy \(\forall x\in R\) thì \(f\left(x\right)=f\left(-x\right)\)
Đúng 1
Bình luận (0)
\(a.f\left(3\right)=4.3^2-5=31.\\ f\left(\dfrac{-1}{2}\right)=4.\left(\dfrac{-1}{2}\right)^2-5=-4.\)
\(b.f\left(x\right)=-1.\Rightarrow4x^2-5=-1.\\ \Leftrightarrow4x^2=4.\Leftrightarrow x^2=1.\\ \Leftrightarrow x=\pm1.\)
\(c.f\left(x\right)=f\left(-x\right).\\ \Rightarrow4x^2-5=4\left(-x\right)^2-5.\\ \Leftrightarrow4x^2-5=4x^2-5.\)
\(\Leftrightarrow0x=0\) (luôn đúng).
Vậy với mọi x ∈ R thì f (x)= f (-x).
Đúng 0
Bình luận (0)
a) Do \( y=f(x)=4x² - 5 \) nên :
\(+) f(3) = 4 . 3^2 - 5 = 4 . 9 - 5 = 36 - 5 = 31 \)
\(+) f(\dfrac{1}{2}) = 4 . (\dfrac{1}{2})^2 - 5 = 4 . \dfrac{1}{4} - 5 = 1 - 5 = -4 \)
Vậy : \(f(3) = 31 ; f(\dfrac{1}{2}) = -4 \)
b) Do \(f(x) = -1 \)
Mà \(f(x) = 4x^2 - 5 \)
\(=> \) \(4x^2 - 5 = -1 \)
\(=> 4x^2 = -1 + 5 \)
\(=> 4x^2 = 4 \)
\(=> x^2 = 1 \) \(= 1^2 = ( -1)^2 \)
\(=> x \) ∈ { -1 ; 1 }
Vậy với \(f(x) = -1 \) thì x ∈ { -1 ; 1 }
c) Ta có : Do \(x^2 = ( -x )^2 \)
\(=> \) \(4x^2 = 4(-x)^2 \)
\(=> 4x^2 - 5 = 4( -x )^2 - 5 \)
\(=> f(x) = f(-x) \)
Vậy với mọi x ∈ R thì \(f(x) = f(-x)\)
Đúng 0
Bình luận (0)
Tìm giá trị thực của m để hàm số F(x) x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) 3x2 – 12x – 4 với mọi
x
∈
ℝ
A.
m
3
2
B.
m
-
9
2
C.
m
9
2
D.
m...
Đọc tiếp
Tìm giá trị thực của m để hàm số F(x) = x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) = 3x2 – 12x – 4 với mọi x ∈ ℝ
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Đồ thị hàm số yf(x) như hình vẽ bên dưới Tìm m để bất phương trình
m
-
x
≥
2
f
x
+
2
+
4
x
+
3
nghiệm đúng với mọi
x
∈
-
3
;...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
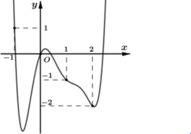
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Đáp án B
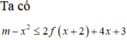
![]()
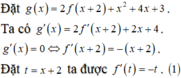
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
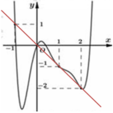
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có



Đúng 0
Bình luận (0)
a) Cho hàm số y = f(x) = \(3x^2+2\). Chứng minh rằng với mọi x thì f(-x) = f(x)
b)Cho hàm số y= f(x) = \(4x^3-2x.\)Chứng minh rằng với mọi x thì f(-x) = -f(x)
a) \(y=f\left(x\right)=3\left(x^2+\frac{2}{3}\right)\)
\(f\left(-x\right)=3\left[\left(-x\right)^2+\frac{2}{3}\right]=f\left(x\right)^{\left(đpcm\right)}\)
b) Đề sai,thay x = 3 vào là thấy.
Đúng 0
Bình luận (0)
Cho hàm số y f x .Xác định với mọi số thực x thoải mãn x 1 ×f x x 4 ×f x 8 với mọi x.Tính f 17 f 41
Xem chi tiết
Cho hàm số yf(x) có f(x)0 với mọi x. Tìm tập hợp tất cả các giá trị thực của x để
f
1
x
f(1) A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) có f'(x)>0 với mọi x. Tìm tập hợp tất cả các giá trị thực của x để f 1 x < f(1)
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hàm số ![]() có
có ![]() thì đồng biến trên R.
thì đồng biến trên R.
Khi đó ta có
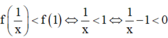
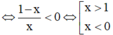
Vậy ![]()
Chọn B
Đúng 0
Bình luận (0)
a,Tìm x, y, z biết 3x 2y; 5x3z và x2+ y2+ z2 68b, Tìm x,y biết|x^2-y^2|+left(x+2right)^20c, Cho hàm số yf(x)ax+b xác định a,b biết f(1)3; f(-1)1d, Cho hàm số yf(x)4x2+3x+5 Tính f(0); f(-1); fleft(frac{-1}{2}right) Chứng minh rằng: f(x)⋮3với mọi x nguyên tố lớn hơn 3
Đọc tiếp
a,Tìm x, y, z biết 3x= 2y; 5x=3z và x2+ y2+ z2= 68
b, Tìm x,y biết\(|x^2-y^2|+\left(x+2\right)^2=0\)
c, Cho hàm số y=f(x)=ax+b xác định a,b biết f(1)=3; f(-1)=1
d, Cho hàm số y=f(x)=4x2+3x+5
Tính f(0); f(-1); \(f\left(\frac{-1}{2}\right)\)
Chứng minh rằng: f(x)\(⋮3\)với mọi x nguyên tố lớn hơn 3
a) (1- x2). ( 4x+5/x-1 - 9/x-1)b. x2 + xy - 2x - 2y Câu 5. Cho hàm số: y (2m+1)x - 3 a. Với m3. Tính f (-3); f(0) b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số. c. Vẽ đồ thị hàm số với m 1 d. Tìm điều kiện để hàm số là hàm bậc nhất. e. Tìm m để hàm số song song với đường thẳng y 5x+1
Đọc tiếp
a) (1- x2). ( 4x+5/x-1 - 9/x-1)
b. x2 + xy - 2x - 2y
Câu 5. Cho hàm số: y = (2m+1)x - 3
a. Với m=3. Tính f (-3); f(0)
b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số.
c. Vẽ đồ thị hàm số với m= 1
d. Tìm điều kiện để hàm số là hàm bậc nhất.
e. Tìm m để hàm số song song với đường thẳng y= 5x+1
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
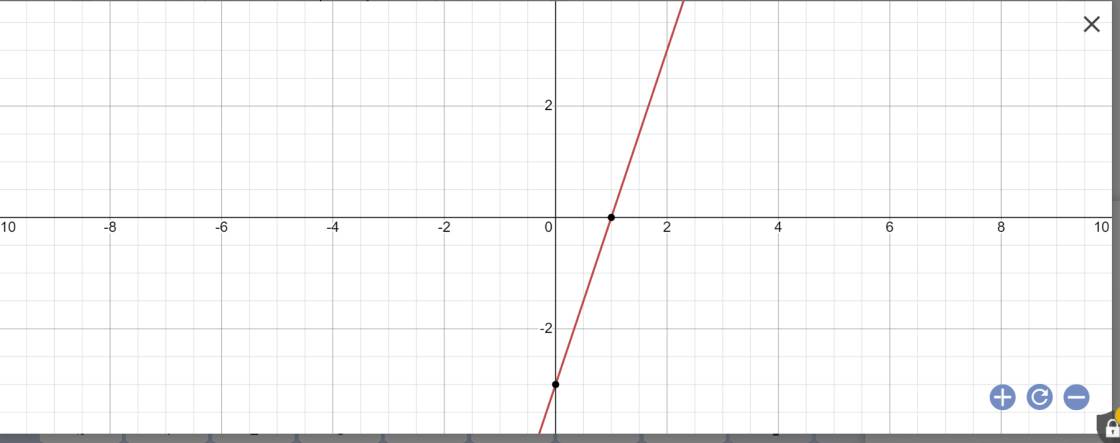
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) =4x\(^2\)- 3
a, tính f(-2)
b, tìm x để f(x) = 1
c, tìm x để f(x) = x
Mọi người giải hộ mình với ạ
a) Có: y = f(x) = 4x2 - 3
=> f(-2) = 4 . (-2) - 3
= -11
Vậy f(-2) = -11
b) Có: f(x) = 4x2 - 3
Mà f(x) = 1
=> 4x2 - 3 = 1
<=> 4x2 = 4
<=> x2 = 1
<=> x = 1 hoặc x = -1
Vậy x = 1 hoặc x = -1 thì f(x) = 1.
c) Có: f(x) = 4x2 - 3
Mà f(x) = x
=> 4x2 - 3 = x
<=> 4x2 - 3 - x = 0
<=> (4x2 + 3x) - (4x + 3) = 0
<=> x(4x + 3) - (4x+ 3) = 0
<=> (x - 1)(4x + 3) = 0
<=> x - 1 = 0 hoặc 4x + 3 = 0
<=> x = 1 hoặc 4x = -3
<=> x = 1 hoặc x = \(-\frac{3}{4}\)
Vậy x = 1 hoặc x = \(-\frac{3}{4}\) thì f(x) = x.
Linz
a, \(f\left(-2\right)=4\left(-2\right)^2-3=16-3=13\)
b, \(f\left(x\right)=1\)hay \(f\left(x\right)=4x^2-3=1\)
\(\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\)
c, \(f\left(x\right)=x\)hay \(4x^2-3=x\)
\(\Leftrightarrow4x^2-3-x=0\Leftrightarrow3x^2+x^2-3-x=0\)
\(\Leftrightarrow3\left(x^2-1\right)+x\left(x-1\right)=0\)
\(\Leftrightarrow3\left(x-1\right)\left(x+1\right)+x\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[3\left(x+1\right)+x\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x+3\right)=0\Leftrightarrow x=1;-\frac{3}{4}\)





















