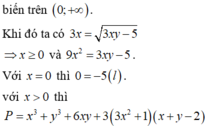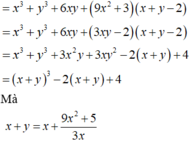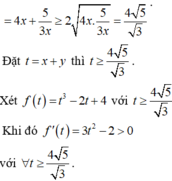Cho 2 số thực phân biệt x,y thỏa mãn x3 + y3 +6xy =8. Tính x+y

Những câu hỏi liên quan
a) Tìm x,y thỏa mãn x3+y3 +1=3xy tính P= (1+1/x)(1+1/y)(x+y)
b) Cho a+2b+c=0 Tính P= a2/2ab + 4b2/ac + c2/2ab
c) Cho x,y Thỏa mãn x3+y3+8=6xy Tính P=(1 + z/y)(1 + z/x)(x+y)
giúp mik với ạ cảm ơn nhiều nhiều!!!
Cho hai số thực x,y thỏa mãn:
9
x
3
+
(
2
-
y
3
x
y
-
5
)
x
+
3
x
y
-...
Đọc tiếp
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )
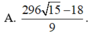
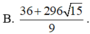
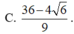
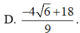
a, Phân tích thành nhân tử (x+y+z)3-x3-y3-z3
b, Cho các số x, y, z thỏa mãn với điều kiện : x+y+z=1 và x3+y3+z3=1
c, Tính giá trị của biểu thức : A= x2001+ y2001+ z2001
a: (x+y+z)^3-x^3-y^3-z^3
=(x+y+z-x)(x^2+2xy+y^2-x^2-xy-xz+z^2)-(y+z)(y^2-yz+z^2)
=(x+y)(y+z)(x+z)
b: x^3+y^3+z^3=1
x+y+z=1
=>x+y=1-z
x^3+y^3+z^3=1
=>(x+y)^3+z^3-3xy(x+y)=1
=>(1-z)^3+z^3-3xy(1-z)=1
=>1-3z-3z^2-z^3+z^3-3xy(1-z)=1
=>1-3z+3z^2-3xy(1-z)=1
=>-3z+3z^2-3xy(1-z)=0
=>-3z(1-z)-3xy(1-z)=0
=>(z-1)(z+xy)=0
=>z=1 và xy=0
=>z=1 và x=0; y=0
A=1+0+0=1
Đúng 2
Bình luận (0)
Cho các số thực x, y , z thỏa mãn 2 điều kiện :
a) (x + y) ( y + z)( z + x) = xyz
b) (x3 + y3 ) (y3 + z3) ( x3 + z3) = x3y3z3
CMR: xyz =0
Có bao nhiêu số thực m để đường thẳng y(m-6)x-4 cắt đồ thị hàm số
y
x
3
+
x
2
-
3
x
-
1
tại ba điểm phân biệt có tung độ
y
1
,
y
2
,
y
3
thỏa mãn
1
y
1...
Đọc tiếp
Có bao nhiêu số thực m để đường thẳng y=(m-6)x-4 cắt đồ thị hàm số y = x 3 + x 2 - 3 x - 1 tại ba điểm phân biệt có tung độ y 1 , y 2 , y 3 thỏa mãn 1 y 1 + 4 + 1 y 2 + 4 + 1 y 3 + 4 = 2 3
A. 2
B. 0
C. 3
D. 1
Phương trình hoành độ giao điểm:
![]()
![]()
Gọi x 1 , x 2 , x 3 là ba nghiệm phân biệt của phương trình này ta có
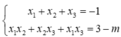 và tung độ các giao điểm là
y
1
=
m
-
6
x
1
-
4
;
y
2
=
m
-
6
x
2
-
4
;
y
3
=
m
-
6
x
3
-
4
;
Vậy điều kiện bài toán:
và tung độ các giao điểm là
y
1
=
m
-
6
x
1
-
4
;
y
2
=
m
-
6
x
2
-
4
;
y
3
=
m
-
6
x
3
-
4
;
Vậy điều kiện bài toán:
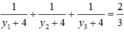
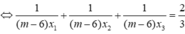
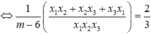
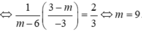
Thử lại ![]() có 3 nghiệm hân biệt nên m = 9 thỏa mãn.
có 3 nghiệm hân biệt nên m = 9 thỏa mãn.
Chọn đáp án D.
*Phương trình a x 3 + b x 2 + c x + d = 0 có ba nghiệm x 1 , x 2 , x 3 thì
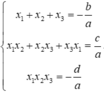
Đúng 0
Bình luận (0)
Cho các số thực dương x, y, z thỏa mãn x3 + y3 + z3 = 24. Tìm GTNN của biểu thức
\(M=\dfrac{xyz+2\left(x+y+z\right)^2}{xy+yz+zx}-\dfrac{8}{xy+yz+zx+1}\)
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Cho hai số thực phân biệt x, y thỏa mãn: 3x2 - 4xy + y2 = 3x - 3y. Tính giá trị của biểu thức: 9x2 - 6xy + y2 + y - 3x + 4
Ta có: \(3x^2-4xy+y^2=3x-3y\)
\(\Leftrightarrow2x^2-2xy+\left(x^2-2xy+y^2\right)=3\left(x-y\right)\)
\(\Leftrightarrow2x\left(x-y\right)+\left(x-y\right)^2-3\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(2x+x-y-3\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(3x-y-3\right)=0\Leftrightarrow\orbr{\begin{cases}x=y\\3x-y=3\end{cases}}\)
Vì x và y là 2 số thực phân biệt nên TH x=y không xảy ra\(\Rightarrow3x-y=3\)
Lại có: \(9x^2-6xy+y^2+y-3x+4=\left(3x-y\right)^2+y-3x+4\)
\(=\left(3x-y\right)^2-\left(3x-y\right)+4\)
Ta thay \(3x-y=3\)vào biểu thức trên:
\(\Rightarrow\left(3x-y\right)^2-\left(3x-y\right)+4=3^2-3+4=9+1=10\)
Vậy giá trị cần tìm của biểu thức đó là 10.
Đúng 0
Bình luận (0)
Cho hai số thực phân biệt x, y thỏa mãn: 3x2 - 4xy + y2 = 3x - 3y. Tính giá trị của biểu thức: 9x2 - 6xy + y2 + y - 3x + 4