john viết một số tự nhiên vào mỗi ô trong 4 ô ở hàng dưới cùng của sơ đồ. Sau đó, anh ta viết vào mỗi ô khác tổng của hai số vào ô ngay bên dưới . Số lượng các số lẻ lớn nhất có thể xuất hiện trong sơ đồ hoàn chỉnh là bao nhiêu ?

Những câu hỏi liên quan
Trong mỗi ô vuông của bảng ô vuông kích thước n\(\times\)n (n là số nguyên dương lẻ) ta viết một trong hai số 1 và -1, một cách tùy ý. Dưới mỗi cột ta viết tích tất cả các số trong cột đó, về phía bên phải của mỗi hàng ta viết tích tất cả các số của hàng đó. Chứng minh rằng tổng tất cả 2n tích vừa viết là một số khác 0.
Gọi tích tất cả các số của mỗi hàng lần lượt là \(a_1,a_2,...,a_n\) và tương ứng số số bằng -1 ở mỗi hàng này lần lượt là \(m_1,m_2,...,m_n\). Khi đó \(a_i=\left(-1\right)^{m_i},\forall i\in\overline{1,n}\).
Tương tự gọi tích tất cả các số ở mỗi cột lần lượt là \(b_1,b_2,...,b_n\) và tương ứng số số bằng -1 ở mỗi cột này lần lượt là \(p_1,p_2,...,p_n\) thì \(b_i=\left(-1\right)^{p_i}.\forall i\in\overline{1,n}\).
Dễ thấy \(m_1+m_2+...+m_n=p_1+p_2+...+p_n\).
Giả sử tổng tất cả 2n tích đó bằng 0.
Khi đó \(\left(-1\right)^{m_1}+\left(-1\right)^{m_2}+...+\left(-1\right)^{m_n}+\left(-1\right)^{p_1}+\left(-1\right)^{p_2}+...+\left(-1\right)^{p_n}=0\).
Gọi x là số số chẵn trong các số \(m_1,m_2,...,m_n\) và y là số số chẵn trong số \(p_1,p_2,...,p_n\).
Ta có \(0=\left(-1\right)^{m_1}+\left(-1\right)^{m_2}+...+\left(-1\right)^{m_n}+\left(-1\right)^{p_1}+\left(-1\right)^{p_2}+...+\left(-1\right)^{p_n}=x-\left(n-x\right)+y-\left(n-y\right)=2\left(x+y\right)-2n\)
\(\Rightarrow x+y=n\).
Mà n lẻ nên x, y khác tính chẵn, lẻ.
Giả sử x chẵn, y lẻ. Khi đó \(m_1+m_2+...+m_n\) là số lẻ và \(p_1+p_2+...+p_n\) là số chẵn, vô lí.
Vậy...
Đúng 1
Bình luận (0)
Cho 64 ô vuông xếp thành một hàng ngang. Viết vào mỗi ô một số tự nhiên bất kì từ 1 đến 16. Ghép thành từng cặp hai ô ở đầu và cuối và các ô cách đều hai ô ở đầu và cuối. Chứng minh rằng tồn tại hai cặp có tổng các số ở hai ô trong mỗi cặp bằng nhau
Thay mỗi dấu “?” bằng số thích hợp để hoàn thiện sơ đồ Hình 1.11, biết số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới.

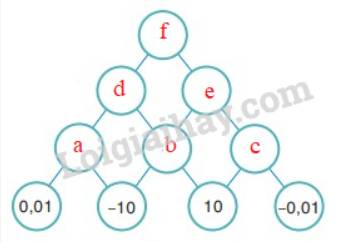
Theo quy luật bài cho, ta được:
a = 0,01 . (-10) = -0,1
b = (-10) . 10 = -100
c = 10 . (-0,01) = -0,1
d = a.b = (-0,1) . (-100) = 10
e = b.c = (-100) . (-0,1) = 10
f = d.e = 10 . 10 = 100
Như vậy:
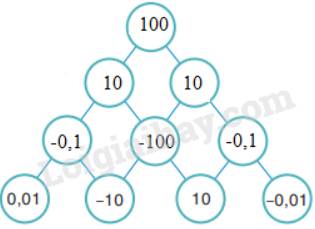
Đúng 0
Bình luận (0)
trong một bảng ô vuông gồm có 5x5 ô vuông, người ta viết vào mỗi ô chỉ một trong 3 số 1;0 hoặc -1. Chứng minh rằng trong các tổng của 5 số theo mỗi cột, mỗi hàng, mỗi đường chéo phải có ít nhất 2 tổng số bằng nhau.
bài này cũng khá khó gặm but đối với anh thì khác!
Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:\(-5\le S\le5\)
\(\Rightarrow\)có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
Bài toán được chứng minh_._
Đúng 0
Bình luận (0)
Vì bảng ô vuông có kích thước 5x5 nên có tất cả:5 hàng,5 cột,2 đường chéo nên có tất cả 12 tổng.
Do khi điền vào các ô là các số 0,1,-1 nên mỗi tổng(S) là một số nguyên thỏa mãn:−5≤S≤5
⇒có 11 giá trị trong khi đó có 12 tổng nên theo nguyên lý Đi-rích-lê(hay còn gọi là chuồng thỏ) thì tồn tại ít nhất 2 tổng có giá trị bằng nhau.
(ĐPCM)
Đúng 0
Bình luận (0)
Trên hành tinh của chúng ta đại dương nào lớn nhất? Em hãy điền các số thích hợp vào ô trống để có các đẳng thức đúng. Sau đó, viết các chữ số tương ứng với các chữ số tìm được vào các ô ở hàng dưới cùng, em sẽ trả lời được câu hỏi nêu trên.
Đọc tiếp
Trên hành tinh của chúng ta đại dương nào lớn nhất? Em hãy điền các số thích hợp vào ô trống để có các đẳng thức đúng. Sau đó, viết các chữ số tương ứng với các chữ số tìm được vào các ô ở hàng dưới cùng, em sẽ trả lời được câu hỏi nêu trên.
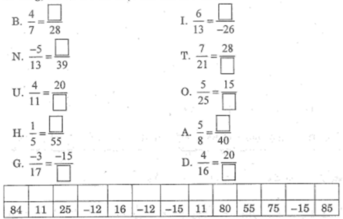
B. 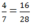 chữ B ứng với số 16
chữ B ứng với số 16
I. 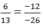 chữ I ứng với số -12
chữ I ứng với số -12
N. 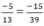 chữ N ứng với số -15
chữ N ứng với số -15
T. 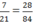 chữ T ứng với số 84
chữ T ứng với số 84
U. 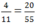 chữ U ứng với số 55
chữ U ứng với số 55
O. 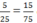 chữ O ứng với số 75
chữ O ứng với số 75
H. 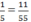 chữ H ứng với số 11
chữ H ứng với số 11
A. 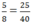 chữ A ứng với số 25
chữ A ứng với số 25
G. 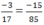 chữ G ứng với số 85
chữ G ứng với số 85
D. 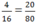 chữ D ứng với số 80
chữ D ứng với số 80

Trên hành tinh của chúng ta, THÁI BÌNH DƯƠNG là đại dương lớn nhất
Đúng 0
Bình luận (0)
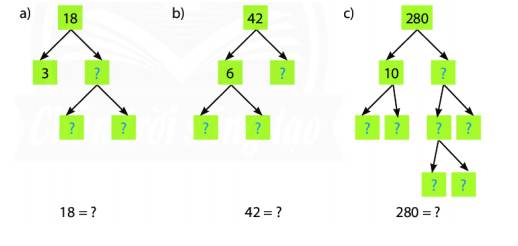
Tìm các số tự nhiên lớn hơn 1 để thay thế dấu trong ô vuông ở mỗi sơ đồ cây dưới đây, rồi viết gọn dạng phân tích ra thừa số nguyên tố của mỗi số 18, 42, 280 bằng cách dùng luỹ thừa.
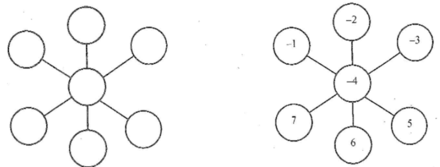
Đố: điền các số -1;-2;-3;-4;5;6;7 vào các ô tròn trong hình bên dưới ( mỗi số vào một ô) sao cho tổng của ba thẳng hàng bất kì đều bằng 0’
Từ các số -1; -2; -3; -4; 5; 6; 7 ta tìm được các bộ ba số có tổng bằng 0 là:
+) ( (-2); (-4); 6) vì (-2) + (-4) + 6 = 0
+) ( (-1); (-4); 5) vì (-1) + (-4) + 5 = 0
+) ((-3); (-4); 7) vì (-3)+ (-4) + 7 = 0
Ba bộ này cùng có chung số -4 nên số đứng ở giữa là – 4.
Ta có cách điền như hình vẽ:
Đúng 0
Bình luận (0)
Người ta định viết các số vào các ô của bảng dưới đây sao cho tổng của 3 số ở 3 ô liền nhau bất kì đều bằng 30Số đc viết ở ô cuối cùng bên phải của bảng sẽ là số mấy?
Đọc tiếp
Người ta định viết các số vào các ô của bảng dưới đây sao cho tổng của 3 số ở 3 ô liền nhau bất kì đều bằng 30
Số đc viết ở ô cuối cùng bên phải của bảng sẽ là số mấy?![]()
![]()
![]()
Trong 1 bảng vuông gồm 5x5 ô vuông người ta viết vào mỗi ô vuông một trong 3 số 1 ; 0 ; -1 sao cho mỗi ô vuông có đúng 1 số CMR : trong các tổng của 5 số theo mỗi cột , mỗi hàng, mỗi đường chéo phải có ít nhất 2 tổng số bằng nhau.
Giá trị nhỏ nhất của mỗi tổng là: -1 + -1 + -1 + -1+ -1 = -5
Giá trị lớn nhất của mỗi tổng là : 1+1+1+1+1=5
=> Số giá trị mà mỗi tổng có thể nhận được là : [5 - (-5) ] +1 = 11 giá trị
có 5 tổng theo hàng ngang, 5 tổng theo hàng dọc, 2 tổng theo hàng chéo
=> có tất cả 12 tổng nhận 11 giá trị
=> theo nguyên lý ĐRL thì có ít nhất 2 tổng bằng nhau
Đúng 0
Bình luận (0)
Mình cũng cần bài này. Thanks LoRd DeMoN.
Đúng 0
Bình luận (0)
anh hc lớp 7 nhưng cũng lm hk ra nek em
Xem thêm câu trả lời
Người ta chia một hình vuông thành 16 ô vuông nhỏ viết vào mỗi ô vuông của bảng một trong các số 0; 1 hoặc 2.Sau đó tính tổng các số theo hàng ngang,cột dọc và đường chéo.Chứng tỏ rằng trong các số đó luôn tồn tại hai tổng có giá trị bằng nhau





















