Hình thang cân ABCD có AB//CD , O là giao điểm của 2 đường chéo
Chứng minh OA = OB , OC = OD
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD.
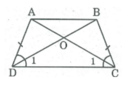
Xét ∆ ADC và ∆ BCD, ta có:
AD = BC (tính chất hình thang cân)
∠ (ADC) = ∠ (BCD) (gt)
DC chung
Do đó: ∆ ADC = ∆ BCD (c.g.c) ⇒ ∠ C 1 = ∠ D 1
Trong ∆ OCD ta có: ∠ C 1 = ∠ D 1 ⇒ ∆ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
hình thang cân ABCD có AB // CD , O là giao điểm của hai đường chéo. Chứng minh rằng OA =OB , OC = OD
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD ?
hình thang cân ABCD có AB//CD , O là giao điểm của hai đường chéo .Chứng minh rằng OA=OB, OC=OD
Xét tam giác OAD và tam giác OBC ta có:
góc OAD = góc OCB (hai góc so le trong, AB//CD)
AD = BC (Vì hình thang cân có hai cạnh bên bằng nhau)
góc ODA = góc OBC (hai góc so le trong, AB//CD)
=> tam giác OAD = tam giac OBC (g-c-g)
=> OA=OB
chứng minh tương tự ta sẽ được OD=OC
Bài làm :
Xét tam giác ABC và tam gác BAD có :
AB cạnh chung
BC = AC ( ABCD httg cân )
AC = BD ( 1 ) ( ABCD httg cân )
\(\Rightarrow\)tam giác ABC = tam giác BAD ( c - c - c )
\(\Rightarrow\widehat{A1}\)= \(\widehat{D1}\)
\(\Rightarrow\)Tam giác OAB cân tại O
\(\Rightarrow\)OA = OB ( 2 )
ta có : OA + OC = AC ( 3 )
OB + OD = BD ( 4 )
Từ ( 1 ) : ( 2 ) ; ( 3 ) ; ( 4 ) suy ra OC = OD
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, AD>BC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D=60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình thang bằng 20cm.
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE
a) Tứ giác BDEC là hình gì ? Vì sao?
b) Các điểm D,E ở vị trí nào thì BD=DE=EC?
Mình đang cần gấp. Giúp mình nhé cảm ơn các bạn
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, AD>BC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D=60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình thang bằng 20cm.
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE
a) Tứ giác BDEC là hình gì ? Vì sao?
b) Các điểm D,E ở vị trí nào thì BD=DE=EC?
Mình đang cần gấp. Giúp mình nhé cảm ơn các bạn
Hình thang cân ABCD có AB//CD.Gọi O là giao điểm của 2 đường chéo. CMR: OA=OB, OC=OD
Xét ΔABD và ΔBAC có:
AB: cạnh chung
AD=BC(gt)
BD=AC(gt)
=>ΔABD=ΔBAC (c.c.c)
=>^ADB=^BCA ;
^ABD=^BAC.
=>ΔOAB cân tại O
=>OA=OB
Có: ^D=^ADB+^BDC
^C=^BCA+^ACD
Mà: ^D=^C(gt) ; ^ADB=^BCA(cmt)
=>^BDC=ACD
=>ΔODC cân tại O
=>OD=OC
Cho hình thang cân ABCD có AB//CD, o là giao điểm của hai đường chéo, e là đường thẳng chứa cạnh bên AD và BC. CMR:
a, OA=OB, OC=OD
b, CM: EO là đường trung trực của 2 đáy hình thang ABCD
Cho hình thang cân ABCD ( AB//CD). Gọi O là giao điểm của 2 đường chéo.
a) Chứng minh OA=OB, OC=OD
b) Giả sử AB<CD, gọi I là giao điểm của AD và BC. Chứng minh IO vuông góc vs CD
Giúp mk giải câu b nha 😀
Bài 1: cho hình thang cân ABCD có AB<CD,o là giao điểm của hai đường chéo,E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC.Cm
a,OA=OB,OC=OD
b,EO là đường trung trực của hai đáy hình thang ABCD
a ) Xét ADC và BCD, ta có:
AD = BC (tính chất hình thang cân)
(ADC) = (BCD) (gt)
DC chung
Do đó: ADC = BCD (c.g.c) ⇒ =
Trong OCD ta có: = ⇒ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
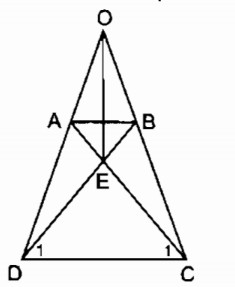
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.