Gọi I là gđ của AC và BD
Theo bất đẳng thức trong tam giác có:
\(AB< IB+IA\) (1)
\(CD< ID+IC\)(2)
Do đó từ (1) và (2) có:
\(AB+CD< IA+IB+IC+ID\)
\(\Leftrightarrow AB+CD< \left(IA+IC\right)+\left(IB+ID\right)\)
\(\Leftrightarrow AB+CD< AC+DB\)
(hình bạn tự vẽ nha )

gọi giao điểm của AC và BD là M
xét \(\Delta ABM\) có \(AM+BM>AB^{\left(1\right)}\)

xét \(\Delta DCM\) có\(DM+MC>DC^{\left(2\right)}\)
Từ \(^{\left(1\right)},^{\left(2\right)}\) ta có
\(AM+MC+BM+MD>AB+CD\)
hay \(AC+BD>AB+CD\) (đpcm)

chưa học nha sr

Gọi giao điểm của AC và BD là O

Ta có:

OA+OB>AB ( bất đẳng thức tam giác)

OC+OD>CD ( bất đẳng thức tam giác)

=> AC+BD>AB+CD

Mà AC+CD>=AB+BD ( giả thiết)

=> 2AC+BD+CD>2AB+BD+CD

=> 2AC>2AB

=> AC>AB

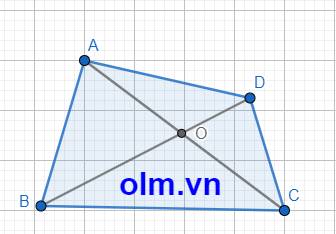
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC 

                                  (AO + OC) + ( OD + OB > AD + BC

                                   AC+ BD > AD + BC 

Chứng Minh tương tự ta có: AC + BD > AB + CD