Cho tam giác ABC vuông tại A có 2 cạnh góc vuông có tỉ lệ là 5:6.Tính tỉ số lượng giác của góc B

Những câu hỏi liên quan
Bài 1 : cho tam giác ABC vuông tại A , AB = 6 , góc B = alpha, biết tan alpha bằng 5/2 . Tính : a, Cạnh AC b, Cạnh BC Bài 2 : Cho tam giác MNP vuông tại P . Hãy viết các tỉ số lượng giác của góc M và góc N . Biết góc M = 40° .
Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
Đúng 2
Bình luận (0)
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)
Đúng 1
Bình luận (0)
4. Chu vi của 1 tam giác vuông là 120cm . Hai cạnh góc vuông tỉ lệ với các số 5 và 12. Tính các cạnh của tam giác vuồng.
5. Cho tam giác ABC có chu vi 180cm và các cạnh AB , AC và BC có độ dài tỉ lệ với các số 12,5,13
a) Tính các cạnh tam giác ABC
b) Tam giác ABC là tam giác gì ? Vì sao ?
4) ti lê canh huyen la: 52 + 122 = 132
ta có AB/5 =AC/12 = BC/13 =>AB=20;AC=48;BC=52
5) cac canh bang 20;48 ;52
la tg vuong vi 522 = 482+202.
( giai toan giup bạn )
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông :
a) Viết các tỉ số lượng giác của góc B ,góc C
b) tính mỗi cạnh góc vuông theo cạnh huyền và các tỉ số lượng giác của góc B ,góc C
c) tính mỗi cạnh góc vuông theo cạnh góc vuông còn lại và các tỉ số lượng giác của góc B ,góc C
Xem chi tiết
cho tam giác abc vuông tại a có cạnh huyền bằng 26.các cạnh góc vuông tỉ lệ với 5 và 12.tính diện tích tam giác abc .
Đặt a/5=b/12=k
=>a=5k; b=12k
Theo đề, ta có: \(25k^2+144k^2=26^2=676\)
=>k=2
=>a=10; b=24
\(S=\dfrac{ab}{2}=\dfrac{10\cdot24}{2}=10\cdot12=120\left(đvdt\right)\)
Đúng 1
Bình luận (0)
đề 1:
Cho tam giác ABC vuông tại A, AH vuông góc BC,AB=30cm,AH=24cm.
a)tính BH?BC?
b)tính các tỉ số lượng giác của các góc của tam giác AHB
đề 2
cho tam giác ABC vuông tại A, AH vuông góc BC , HB=4cm, HC=9cm
a)tính các cạnh tam giác ABC
b)tính các góc của tam giác ABC
Cho tam giác ABC vuông tại A có góc B=60độ. Cạnh BC=2a. Hãy tính tỉ số lượng giác của góc 30độ và góc 60độ.
Cho tam giác ABC vuông tại A có cạnh AB = 5cm, cạnh huyền dài hơn AC là 1cm.
a, Tính các tỉ số lượng giác của các góc B và C.
b, Tìm số đo các góc của tam giác ABC.
Cho tam giác ABC vuông cân tại A có cạnh góc vuông=a.Tính tỉ số lượng giác góc B
Lời giải
Các tỉ số lượng giác của góc β là:
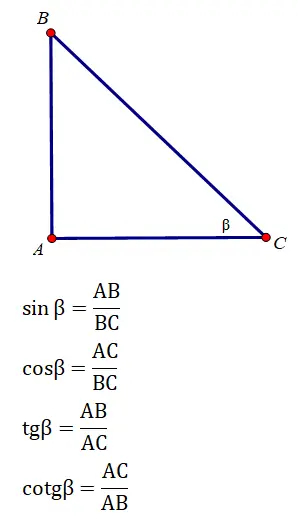
Theo pitago thì BC= căn 2a^2 = căn 2 . a
Khi đó sinB = a/căn 2 . a = căn 2
cosB = sinB = căn 2
tanB = a/a = 1
cotB = tan B = 1
Vậy ta có : ...
xong
Cho tam giác ABC vuông tại A có BC bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12.Tính độ dài các cạnh góc vuông AB và AC?
Cho tứ giác ABCD có A=700,B=1000,các tia phân giác của góc C và D cắt nhau tại O.Tính số đo COD
giúp mình với mình đang cần gấp ạ
a: Đặt \(\dfrac{AB}{5}=\dfrac{AC}{12}=k\)
=>AB=5k; AC=12k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(25k^2+144k^2=26^2\)
=>\(k^2=4\)
=>k=2
=>AB=10cm; AC=24cm
b: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-70^0=290^0\)
=>\(2\cdot\left(\widehat{ODC}+\widehat{OCD}\right)=290^0\)
=>\(\widehat{OCD}+\widehat{ODC}=145^0\)
Xét ΔOCD có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^0\)
=>\(\widehat{COD}=180^0-145^0=35^0\)
Đúng 1
Bình luận (0)















