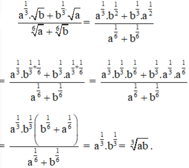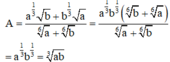rút gọn bt √b6*(7-b)2

Những câu hỏi liên quan
Rút gọn các biểu thức sau:
a
1
3
.
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Rút gọn các biểu thức sau: a 1 3 . b + b 1 3 a a 6 + b 6
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6 .
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Đáp án B.
Ta có A = a 1 3 b + b 1 3 a a 6 + b 6 = a 1 3 b 1 3 b 6 + a 6 a 6 + b 6 = a 1 3 b 1 3 = a b 3 .
Đúng 0
Bình luận (0)
Cho a, b là các số thực dương. Rút gọn biểu thức
P
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho a, b là các số thực dương. Rút gọn biểu thức P = a 1 3 b + b 1 3 a a 6 + b 6
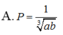
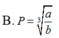
![]()
![]()
Cho a, b là các số thực dương. Rút gọn biểu thức
P
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho a, b là các số thực dương. Rút gọn biểu thức P = a 1 3 b + b 1 3 a a 6 + b 6
A. P = 1 a b 3
B. P = a b 3
C. P = a b 3
D. P = a 3 b 3 3
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+
b
6
A.
A...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6
A. A = a b 6
B. A = a b 3
C. A = 1 a b 3
D. A = 1 a b 6
Cho hai số thực dương a và b. Rút gọn biểu thức
A
a
1
3
b
+
b
1
3
a
a
6
+
b
6
....
Đọc tiếp
Cho hai số thực dương a và b. Rút gọn biểu thức A = a 1 3 b + b 1 3 a a 6 + b 6 .
A. A = a b 6
B. A = a b 3
C. 1 a b 3
D. 1 a b 6
Đáp án B
Sử dụng máy tính tính giá trị của A với a=2;b=3 rồi lưu vào biến X:


Với A:


Kết quả ra khác 0 nên ta loại A.
Với B:
![]()

Vậy ta chọn B.
Đúng 0
Bình luận (0)
1 cho biểu thức A=5x(xy^2-2xy)-5x^2y^2. Rút gọn A .b) Tính GT của A khi x=-1/2 ,y=2
2. Tìm GTLN của bt A = |x-7|-|x-9|.Q= |x-2|+|x-8| b) tìm GTLN của bt P= 9-2|x-3|
a, rút gọn bt: 3×(2x + 1)+2× (3x - 7)
b, tính giá trị biểu thức M= 8x3 - 12x2y+ 6xy2-y3
Cho bt A=2x^2+4x/x^3-4x +x^2-4/x^2 +2x +2/2-x
a,Rút gọn bt A
b, Tính giá trị bt A khi x =4
\(A=\frac{2x^2+4x}{x^3-4x}+\frac{x^2-4}{x^2+2x}+\frac{2}{2-x}\left(x\ne0;x\ne\pm2\right)\)
\(A=\frac{2x^2+4x}{x\left(x^2-4\right)}+\frac{\left(x-2\right)\left(x+2\right)}{x\left(x+2\right)}-\frac{2}{x-2}\)
\(A=\frac{2x^2+4x}{x\left(x-2\right)\left(x+2\right)}+\frac{\left(x-2\right)^2\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}-\frac{2x\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}\)
\(A=\frac{2x^2+4x}{x\left(x-2\right)\left(x+2\right)}+\frac{x^3-2x^2-4x+8}{x\left(x-2\right)\left(x+2\right)}-\frac{2x^2+4x}{x\left(x-2\right)\left(x+2\right)}\)
\(A=\frac{2x^2+4x+x^3-2x^2-4x+8-2x^2-4x}{x\left(x-2\right)\left(x+2\right)}\)
\(A=\frac{-2x^2-4x+8}{x\left(x-2\right)\left(x+2\right)}=\frac{-2x\left(x+2\right)+8}{x\left(x-2\right)\left(x+2\right)}=\frac{-2x+8}{x\left(x-2\right)}\)
Vậy \(A=\frac{-2x+8}{x\left(x-2\right)}\left(x\ne0;x\ne\pm2\right)\)
b) \(A=\frac{-2x+8}{x\left(x-2\right)}\left(x\ne0;x\ne\pm2\right)\)
Ta có: x=4 (tmđk) thay vào A ta có:
\(A=\frac{-2\cdot4+8}{4\left(4-2\right)}=\frac{-8+8}{4\cdot2}=\frac{0}{8}=0\)
Vậy A=0 với x=4