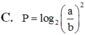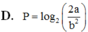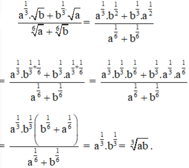Các câu hỏi tương tự
Rút gọn các biểu thức sau:
a
1
3
.
b
-
1
3
-
a
-
1...
Đọc tiếp
Rút gọn các biểu thức sau: a 1 3 . b - 1 3 - a - 1 3 . b 1 3 a 2 3 - b 2 3
Rút gọn biểu thức
A
a
4
-
2
log
a
b
(
a
0
;
a
≠
1
;
b
0
)
A. B. C. D.
Đọc tiếp
Rút gọn biểu thức A = a 4 - 2 log a b ( a > 0 ; a ≠ 1 ; b > 0 )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Rút gọn biểu thức
P
a
3
b
3
-
1
3
+
1
.
a
-
1...
Đọc tiếp
Rút gọn biểu thức
P = a 3 b 3 - 1 3 + 1 . a - 1 - 3 b - 2 a , b > 0
![]()
![]()
![]()
![]()
Xét các số phức
z
a
+
b
i
(
a
,
b
∈
ℝ
)
thỏa mãn
z
-
3
-
3
i...
Đọc tiếp
Xét các số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn z - 3 - 3 i = 6 .
Tính P=3a+b khi biểu thức 2 z + 6 - 3 i + 3 z + 1 + 5 i đạt giá trị nhỏ nhất.
A. P= 20
B. P=2+ 20
C. P= - 20
D. P= - 2 - 20
Rút gọn biểu thức
P
(
a
π
+
b
π
)
-
(
4
1...
Đọc tiếp
Rút gọn biểu thức P = ( a π + b π ) - ( 4 1 π a b ) π với a, b là các số dương.
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho a, b là các số thực dương. Rút gọn biểu thức
P
a
1
3
b
+
b
1
3
a
a
6
+...
Đọc tiếp
Cho a, b là các số thực dương. Rút gọn biểu thức P = a 1 3 b + b 1 3 a a 6 + b 6
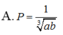
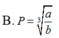
![]()
![]()
Rút gọn biểu thức
P
a
2
b
(
a
b
-
2
)
-
3
(
a
-
2
b
-...
Đọc tiếp
Rút gọn biểu thức P = a 2 b ( a b - 2 ) - 3 ( a - 2 b - 1 ) - 2 viết kết quả sao cho các lũy thừa đều dương
A. P = a 3 b 9
B. P = b a 5
C. P = b a 3
D. P = a b 5
Rút gọn các biểu thức sau:
b
1
5
b
4
5
-
b
-
1
5...
Đọc tiếp
Rút gọn các biểu thức sau: b 1 5 b 4 5 - b - 1 5 b 2 3 . b 3 - b - 2 3
Cho các số thực dương a và b. Rút gọn biểu thức
P
a
-
b
a
4
-
b
4
-
a
+
a
b
4...
Đọc tiếp
Cho các số thực dương a và b. Rút gọn biểu thức P = a - b a 4 - b 4 - a + a b 4 a 4 + b 4 được kết quả là:
A. a 4 - b 4
B. b 4
C. b - a
D. a 4
Với các số thực
a
,
b
0
bất kỳ, rút gọn biểu thức
P
2
log
2
a
log
1
2
b
2
ta được
Đọc tiếp
Với các số thực a , b > 0 bất kỳ, rút gọn biểu thức P = 2 log 2 a = log 1 2 b 2 ta được
![]()
![]()