Hãy dùng thước và compa để vẽ đường thẳng y=\(\sqrt{2}\) .x

Những câu hỏi liên quan
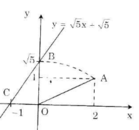
Đồ thị của hàm số y = √3 x + √3 được vẽ bằng compa và thước thẳng (h.8).
Hãy thực hiện cách vẽ đó rồi nêu lại cách thực hiện.
Áp dụng: Vẽ đồ thị của hàm số y = √5 x + √5 bằng compa và thước thẳng.
Hướng dẫn: Tìm điểm trên trục tung có tung độ bằng √5.
Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
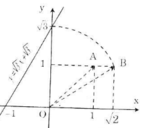
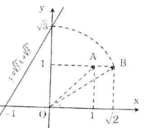
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
Đúng 0
Bình luận (0)
Đồ thị của hàm số y = √3 x + √3 được vẽ bằng compa và thước thẳng (h.8).
Hãy thực hiện cách vẽ đó rồi nêu lại cách thực hiện.
Áp dụng: Vẽ đồ thị của hàm số y = √5 x + √5 bằng compa và thước thẳng.
Hướng dẫn: Tìm điểm trên trục tung có tung độ bằng √5.
a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
Đúng 0
Bình luận (0)
Đồ thị của hàm số ysqrt{3}x+sqrt{3} được vẽ bằng compa và thước thẳng (h.8)
Hãy tìm hiểu cách vẽ đó rồi nêu lại các bước trên
Áp dụng : Vẽ đồ thị của hàm số ysqrt{5}x+sqrt{5} bằng compa và thước thẳng
Hướng dẫn : Tìm điểm trên trục tung có tung độ bằng sqrt{5}
Đọc tiếp
Đồ thị của hàm số \(y=\sqrt{3}x+\sqrt{3}\) được vẽ bằng compa và thước thẳng (h.8)
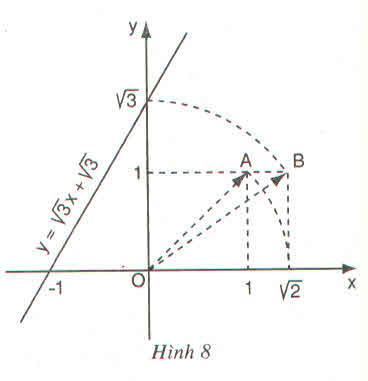
Hãy tìm hiểu cách vẽ đó rồi nêu lại các bước trên
Áp dụng : Vẽ đồ thị của hàm số \(y=\sqrt{5}x+\sqrt{5}\) bằng compa và thước thẳng
Hướng dẫn : Tìm điểm trên trục tung có tung độ bằng \(\sqrt{5}\)
Bài giải:
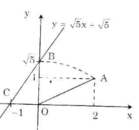
Hình bên diễn tả cách dựng đoạn thẳng có độ dài bằng √5.
Đồ thị hàm số y = √5 x + √5 đi qua hai điểm A(0; √5) và B(-1; 0).
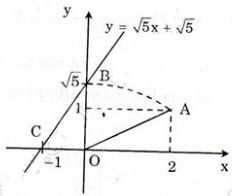
Đúng 0
Bình luận (0)
Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
Cách 1:
Gọi trung điểm BC là M
Ta kẻ xy qua M vuông góc với BC
Cách 2:
Từ B, C vẽ 2 cung tròn có bán kính \(R \ge \dfrac{1}{2}BC \)
2 cung tròn giao nhau tại 2 điểm M, N
Kẻ đường thẳng xy đi qua 2 điểm M, N. Ta được đường trung trực xy đi qua chúng
Đúng 0
Bình luận (0)
Hãy nêu cách vẽ trung điểm của đoạn thẳng AB mà chỉ dùng compa ( không được dùng thước)
giao của 2 hình tròn có tâm là 2 điểm mút và có bán kính = chiều dài đoạn thẳng rồi từ đó, kẻ vuông góc vs đoạn thẳng đó
tick mk nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.3. Vē tia Oz đi qua M.Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Đọc tiếp
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy
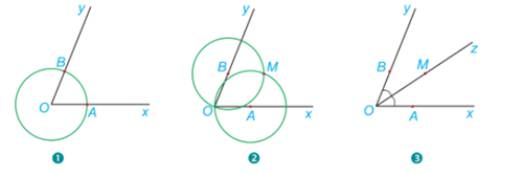
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Xét \(\Delta OBM\) và \(\Delta OAM\) có:
\(OA = OB( = R)\)
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
\( \Rightarrow \)\(\Delta OBM\) = \(\Delta OAM\)(c.c.c)
\( \Rightarrow \) \(\widehat {MOB} = \widehat {MOA}\) (hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Đồ thị hàm số y = √3 x được vẽ bằng compa và thước thẳng ở hình 4. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
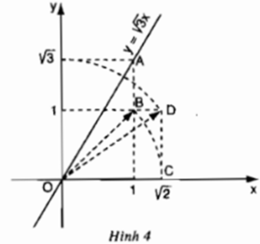
- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
![]()
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
![]()
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.
Đúng 0
Bình luận (0)
Đồ thị hàm số y = √3 x được vẽ bằng compa và thước thẳng ở hình 4. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
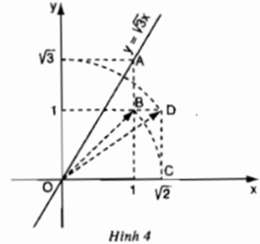
- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
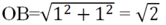
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
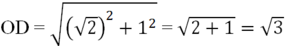
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.
Đúng 0
Bình luận (0)
dùng thước eke để vẽ hình vuông cạnh 7cm vào vở,kẻ thêm hai đường chéo rồi dùng compa đo và so sánh độ dài của chúng