đường thẳng đi qua trung điểm của đường trung bình có đi qua trung điểm của cạnh đáy hay không

Những câu hỏi liên quan
CMR: đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai
Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.
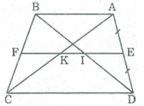
Xét hình thang ABCD có AB // CD.
E là trung điểm AD, đường thẳng đi qua E song song với AB cắt BC tại F, AC tại K, BD tại I.
Vì E là trung điểm AD nên EF// AB
Suy ra: BF = FC (tính chất đường trung bình hình thang)
Trong ∆ ADC ta có: E là trung, điểm của cạnh AD
EK // DC
Suy ra: AK = KC (tính chất đường trung bình của tam giác)
Trong ∆ ABD ta có: E là trung điểm của cạnh AD
EI // AB
Suy ra: BI = ID (tính chất đường trung bình của tam giác)
Vậy đường thẳng song song với 2 đáy, đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm của cạnh bên BC và trung điểm hai đường chéo AC, BD.
Đúng 0
Bình luận (0)
CHỨNG minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai .
Giả sử hình thang là ABCD
trung điểm của cạnh AD là E
EF // AB // DC (F thuộc BC)
Gọi I là gia điểm AC , EF
Ta có
EI//DC (I thuộc EF , EF//DC)
EA=ED
=> EI là đường trung bình của tam giác ACD
=>AI=IC
Ta có
IF//AB (I thuộc EF,EF//AB)
AI=IC (cmt)
=> IF là đường trung bình của tam giác ABC
=>BF=FC
Gọi K là trung điểm BD và EF
ta có
BF=FC
KF//DC(K thuộc EF, EF//DC)
=>KF là đường trung bình của tam giác BDC
=>BK=KD
Xong rồi nha !!!!
1 T I C K nha
____________________________CHÚC BẠN HỌC TỐT _________________________
Đúng 0
Bình luận (0)
Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai
Cho đoạn thẳng AB có trung điểm M. Tập hợp các điểm C sao cho tam giác ABC là tam giác cân có đáy là AB là:
đường trung trực của AB.
một đường thẳng đi qua trung điểm M của AB, không lấy điểm M.
một đường thẳng đi qua trung điểm M của AB.
đường trung trực của AB, không lấy trung điểm M của AB.
CMR đường thẳng đi qua trung điểm 1 cạnh bên hthang và song song vs hai đáy thì đi qua trung điểm canh bên còn lại và đi qua trung điểm 2 đường chéo hình thang
Xem chi tiết
2. CMR đường thẳng đi qua trung điểm 1 dường chéo của hthag và song song với 2 đáythì đi qua trung điểm của đường chéo còn lại và đi qua trung điểm 2 cạnh bên hình thang
(vẽ hình cả 2 hộ mk nha, tks trc :))))
Chọn khăng định sai A. Hai điểm M và N đối xứng với nhau qua đường thẳng AB thì MN là đường trung trực của đoạn thẳng AB B. Đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai đáy là đường trung bình của hình thang đó. C. E đổi xứng F qua O khi O là trung điểm EF D. Đường thẳng đi qua trung điểm hai cạnh của tam giác thì song song với cạnh còn lại.
c/m tính chất sau
Đường thẳng đi qua trung điểm hai cạnh bên của hình thang song song với hai đáy thì đi qua trung điểm 2 đường chéo
ok, vì nó là đg trung bình của hình thang
Đúng 0
Bình luận (0)
Chứng minh rằng một đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì cũng đi qua trung điểm của hai đường chéo.
Vẽ hình thang ABCD, AB song song với CD. Lấy M, N lần lượt là trung điểm của BD và AC. Lấy H và K lần lượt là trung điểm của BC và AD.
Xét tam giác BCD có: - KB = KC (gt)
- MB = MD (gt)
MK là trung bình của BCD.
MK song song và bằng ½ CD
Tương tự như trên ta có:
- HN là trung bình ADC. HN song song và bằng ½ CD.
- HM là trung bình ABD. HM song song và bằng ½ AB.
- KN là trung bình của CAB. KN song song và bằng ½ AB.
H, M, N, K thẳng hàng (tiên đề Ơ – clit)
HK là trung bình của hình thang ABCD (tự chứng minh).
HK = (AB + CD)/2 (t/c)
HM + NK + KM + HN = 2HK.
mà MN = HK – HM – NK
MN = (HM + NK + KM + HN)/2 – HM – NK
= (AB + CD)/2 – AB
= 1/2AB – AB + CD/2
= CD/2 – 1/2AB
= (CD – AB)/2 (đpcm)
Đúng 0
Bình luận (0)

















