Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

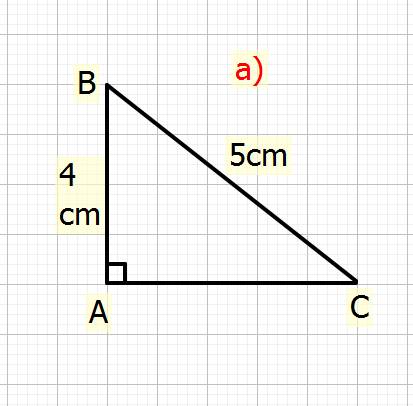
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

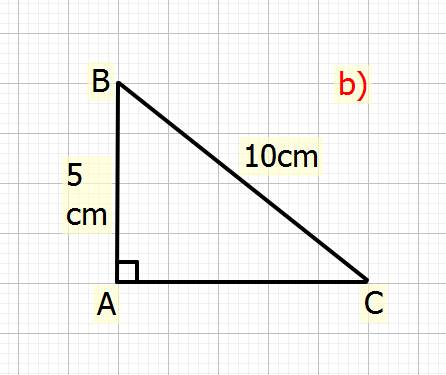
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).

\(\cos C=\sqrt{1-\sin^2C}=\sqrt{1-\frac{9}{25}}=\sqrt{\frac{16}{25}}\)

\(\Rightarrow\cos C=\frac{4}{5}\)

\(\Rightarrow\tan C=\frac{\sin C}{\cos C}=\frac{3}{5}:\frac{4}{5}=\frac{3}{4}\)và \(\cot C=\frac{4}{3}\)

Ta có: \(\widehat{C};\widehat{B}\)là hai góc phụ nhau

\(\Rightarrow\hept{\begin{cases}\sin C=\cos B\\\cos C=\sin B\end{cases};\hept{\begin{cases}\tan C=\cot B\\\cot C=\tan B\end{cases}}}\)

\(\Rightarrow\sin B=\frac{4}{5};\cos B=\frac{3}{5};\tan B=\frac{4}{3};\cot B=\frac{3}{4}\)

Ta có: \(\sin C=\frac{AB}{BC}=\frac{3}{5}\) 

=> \(\frac{AB}{3}=\frac{BC}{5}=k\left(k\inℕ\right)\)

=> \(\hept{\begin{cases}AB=3k\\BC=5k\end{cases}}\)

=> \(AC=\sqrt{\left(5k\right)^2-\left(3k\right)^2}=\sqrt{16k^2}=4k\)

Đến đây thì xong rồi:))

\(\sin B=\frac{AC}{BC}=\frac{4k}{5k}=\frac{4}{5}\) ; \(\cos B=\frac{AB}{BC}=\frac{3k}{5k}=\frac{3}{5}\)

\(\tan B=\frac{AC}{AB}=\frac{4k}{3k}=\frac{4}{3}\) ; \(\cot B=\frac{AB}{AC}=\frac{3k}{4k}=\frac{3}{4}\)

Xét $\Delta ABC$:

$\cos B=\sin C=0,6$

$\cos^2B=0,6.0,6=0,36$

Mà $\cos^2B+\sin^2B=1$

$\Rightarrow \sin^2B=0,64\\\Leftrightarrow \sinB=0,8(vì\,\,\sinB>0)$

$\Rightarrow \sin B=\cos C=0,8$

Ta có: $\tan C=\dfrac{\sin C}{\cos C}=\dfrac{0,6}{0,8}=0,75$

$\cotC=\dfrac{\cosC}{\sinC}=\dfrac{0,8}{0,6}=\dfrac{4}{3}$

Vậy $\sin C=0,6;\cos C=0,8;\tanC=0,75;\cotC=\dfrac{4}{3}$

Tương tự câu 2